题目内容
如图所示，在正方体ABCD-A1B1C1D1中，M为棱CC1的中点，则异面直线BD1与AM所成角的余弦值为
| ||
| 9 |
| ||
| 9 |
分析：分别以
，
，
的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，不妨设正方体的棱长为1，则异面直线BD1与AM所成角的余弦值，转化为求向量
与
的夹角的余弦值，利用向量夹角公式即可求得，注意向量夹角与异面角间的关系．
| DA |
| DC |
| DD1 |
| BD1 |
| AM |
解答：解：分别以
，
，
的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，
不妨设正方体的棱长为1，则A（1，0，0），B（1，1，0），M（0，1，
），D1（0，0，1），
所以
=（-1，-1，1），
=（-1，1，
），
则cos＜
，
＞=
=
=
，即异面直线BD1与AM所成角的余弦值为
，
故答案为：
．
| DA |
| DC |
| DD1 |
不妨设正方体的棱长为1，则A（1，0，0），B（1，1，0），M（0，1，
| 1 |
| 2 |
所以
| BD1 |
| AM |
| 1 |
| 2 |
则cos＜
| BD1 |
| AM |
| ||||
|
|
1-1+
| ||||||
|
| ||
| 9 |
| ||
| 9 |
故答案为：
| ||
| 9 |
点评：本题考查异面直线及其所成角的求解，考查向量运算，属中档题．
练习册系列答案
作业辅导系列答案
相关题目
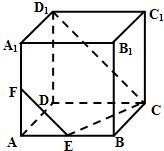如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）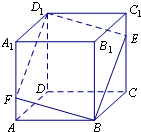
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）