题目内容
(本小题满分14分)已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,求
,求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)证明:对 ,不等式
,不等式 成立.
成立.
(Ⅰ)函数 在
在 上单调递增,在
上单调递增,在 上单调递减; (Ⅱ)详见解析; (Ⅲ)
上单调递减; (Ⅱ)详见解析; (Ⅲ)
【解析】
试题分析:(Ⅰ)先求函数 的导数,再利用导数符号确定函数的单调区间;
的导数,再利用导数符号确定函数的单调区间;
(Ⅱ)由第(Ⅰ)问的结果,根据极值点与区间 的关系对
的关系对 的取值进行分类讨论,从而确定下同条件下的最大值. (Ⅲ)要证:
的取值进行分类讨论,从而确定下同条件下的最大值. (Ⅲ)要证: ,即证:
,即证: ,即证:
,即证:
而由(I)的结果,易知: 对任何
对任何 恒成立,因此可构造函数证明不等式成立.
恒成立,因此可构造函数证明不等式成立.
试题解析:解:(Ⅰ) 的定义域为
的定义域为 ,
, ,
,
由 ,得
,得 .
.
当 时,
时, ;当
;当 时,
时, .
.
所以函数 在
在 上单调递增,在
上单调递增,在 上单调递减. (4分)
上单调递减. (4分)
(Ⅱ)(1)当 ,即
,即 时,
时, 在
在 上单调递增,所以
上单调递增,所以
 .
.
(2)当 时,
时, 在
在 上单调递减,所以
上单调递减,所以
 .
.
(3)当 ,即
,即 时,
时, 在
在 上单调递增,在
上单调递增,在 上单调递减,所以
上单调递减,所以
 . (10分)
. (10分)
(Ⅲ)由(Ⅰ)知,当 时,
时, ,所以在
,所以在 上,恒有
上,恒有
 ,即
,即 且当
且当 时等号成立.
时等号成立.
因此,对 ,恒有
,恒有 .
.
因为 ,
, ,所以
,所以 ,即
,即 ,
,
所以 .
.
即对 ,不等式
,不等式 成立. (14分)
成立. (14分)
考点:1、导数在研究函数性质中的应用;2、利用函数的思想解决不等式的问题.

练习册系列答案
相关题目
计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制数的对应关系如下表:
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:E+D=1B,则B×F (“×”表示通常的乘法运算)等于( )
A.A5 B.BF C.165 D.B9
 的图象, 可能正确的是( )
的图象, 可能正确的是( )
 ,则AC= .
,则AC= .
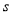 的值为( )
的值为( )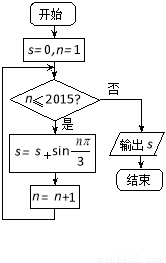
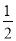 B.
B.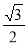 C.
C.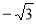 D.0
D.0 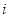 行的第
行的第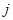 个数对为
个数对为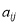 ,如
,如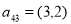 ,则
,则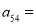 ________;(Ⅱ)
________;(Ⅱ)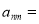 ________.
________. 的直线
的直线 与双曲线
与双曲线 交于不同的两点P、Q,若点P、Q在
交于不同的两点P、Q,若点P、Q在 轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是
轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是  B.2 C.
B.2 C. D.3
D.3  的公比
的公比 ,
, ,
,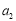 是方程
是方程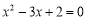 的两根.
的两根.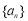 的通项公式;
的通项公式;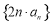 的前
的前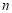 项和
项和 .
.