Question

现有一张长80厘米、宽60厘米的长方形ABCD铁皮，准备用它做成一只无盖长方体铁皮盒，要求材料利用率为l00%，不考虑焊接处损失．
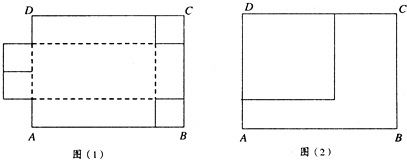
方案一：如图（1），从右侧两个角上剪下两个小正方形，焊接到左侧中闻，沿虚线折起，求此时铁皮盒的体积；
方案二：如图（2），若从长方形ABCD的一个角上剪下一块正方形铁皮，作为铁皮盒的底面，用余下材料剪拼后作为铁皮盒的侧面，求该铁皮盒体积的最大值，并说明如何剪拼？．

Answer 1

方案一：设小正方形的边长为x，由题意得4x=60，x=15，
所以铁皮盒的体积为65×30×15=29250（cm³）． …（4分）
方案二：设底面正方形的边长为x（0＜x＜60），长方体的高为y，
由题意得x²+4xy=4800，即y=

4800-x2

4x

，
所以铁皮盒体积V(x)=x2y=x2

4800-x2

4x

=-

1

4

x3+1200x，…（10分）V/(x)=-

3

4

x2+1200，令V′（x）=0，解得x=40或x=-40（舍），
当x∈（0，40）时，V'（x）＜0；当x∈（40，60）时，V'（x）＞0，
所以函数V（x）在x=40时取得最大值32000cm³．将余下材料剪拼成四个长40cm，宽20cm的小长方形作为正方形铁皮盒的侧面即可．     …（15分）
答：方案一铁皮盒的体积为29250cm³；方案二铁皮盒体积的最大值为32000cm³，将余下材料剪拼成四个长40cm，宽20cm的小长方形作为正方形铁皮盒的侧面即可．（16分）