题目内容
已知函数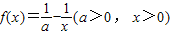
(Ⅰ)判断函数f(x)的单调性并用函数单调性定义加以证明;
(Ⅱ)若f(x)在
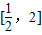 上的值域是
上的值域是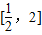 ,求a的值;
,求a的值;(Ⅲ)当m,n∈(0,+∞),若f(x)在[m,n]上的值域是[m,n](m<n),求实数a的取值范围.
【答案】分析:(1)定义法证明函数的单调性;
(2)f(x)在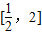 上单调递增,值域是
上单调递增,值域是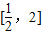 ,则
,则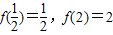 ;
;
(3)f(x)在[m,n]上的值域是[m,n](m<n),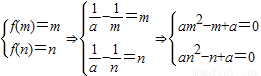 ,方程ax2-x+a=0有两个不等正实数根x1,x2,可得答案.
,方程ax2-x+a=0有两个不等正实数根x1,x2,可得答案.
解答:解:(1)证明:设x2>x1>0,则x2-x1>0,x1x2>0,
∵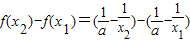 =
=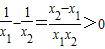 ,
,
∴f(x2)>f(x1),∴f(x)在(0,+∞)上是单调递增的.
(2)∵f(x)在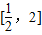 上单调递增,∴
上单调递增,∴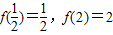 ,易得
,易得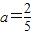 .
.
(3)依题意得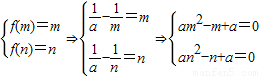
又∵0<m<n,∴方程ax2-x+a=0有两个不等正实数根x1,x2
又∵a>0,对称轴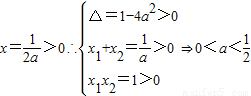
∴实数a的取值范围为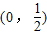 .
.
点评:本题为函数单调性的证明,并利用单调性来解决问题,把方程有两实根转化为二次函数问题是解决问题的关键,属中档题.
(2)f(x)在
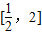 上单调递增,值域是
上单调递增,值域是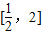 ,则
,则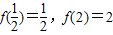 ;
;(3)f(x)在[m,n]上的值域是[m,n](m<n),
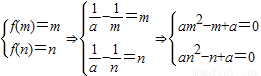 ,方程ax2-x+a=0有两个不等正实数根x1,x2,可得答案.
,方程ax2-x+a=0有两个不等正实数根x1,x2,可得答案.解答:解:(1)证明:设x2>x1>0,则x2-x1>0,x1x2>0,
∵
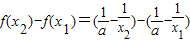 =
=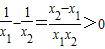 ,
,∴f(x2)>f(x1),∴f(x)在(0,+∞)上是单调递增的.
(2)∵f(x)在
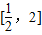 上单调递增,∴
上单调递增,∴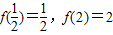 ,易得
,易得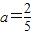 .
.(3)依题意得
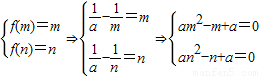
又∵0<m<n,∴方程ax2-x+a=0有两个不等正实数根x1,x2
又∵a>0,对称轴
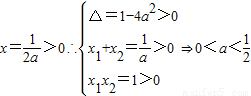
∴实数a的取值范围为
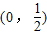 .
.点评:本题为函数单调性的证明,并利用单调性来解决问题,把方程有两实根转化为二次函数问题是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数函f(x)=x|x|-2x (x∈R)
已知函数函f(x)=x|x|-2x (x∈R)