题目内容
已知函数
则
是（ ）
| A．单调递增函数 | B．单调递减函数 |
| C．奇函数 | D．偶函数 |
D
解析试题分析：
=
=
，而
，所以是偶函数，故选D.
考点：1.两角和差公式；2.函数的奇偶性.
练习册系列答案
相关题目
函数
的部分图像如图所示，如果
，且
，则
（ ）
A． | B． | C． | D．1 |
函数
的部分图象如右图所示，设
是图象的最高点，
是图象与
轴的交点，则
（ ）
A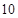． | B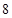． | C． | D． |
.要得到一个奇函数，只需将
的图象（ ）
A．向右平移 个单位 | B．向右平移 个单位 |
| C．向左平移个单位 | D．向左平移个单位 |
在
中，已知
，那么一定是（ ）
| A．等腰直角三角形 | B．等腰三角形 | C．直角三角形 | D．等边三角形 |
已知函数
，直线
是函数
图像的一条对称轴，则
（ ）
A． | B． | C． | D． |
在
中，若
，则的外接圆半径是（ ）
A． | B． | C． | D． |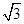
为了得到函数
的图象，只需把函数
的图象( )
A．向左平移 个单位 | B．向左平移 个单位 |
| C．向右平移个单位 | D．向右平移个单位 |