Question

已知各项均不相等的等差数列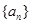的前三项和为18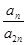，是一个与无关的常数，若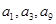恰为等比数列的前三项，（1）求的通项公式．（2）记数列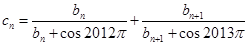，的前三项和为，求证：

 

Answer 1

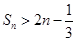
【答案】

（1） ；

（2） 。

【解析】

试题分析：（1）是一个与无关的常数  2分

又  4分

………6分

（2）  8分

又因为

即  12分

所以：  12分

考点：本题主要考查等差中项、等比数列的的基础知识，“放缩法”，不等式的证明。

点评：中档题，本题综合考查等差数列、等比数列的基础知识，本解答从确定通项公式入手，明确了所研究数列的特征。“分组求和法”、“错位相消法”、“裂项相消法”是高考常常考到数列求和方法。先求和，再利用“放缩法”证明不等式，是常用方法。