题目内容
已知函数f(x)=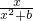 ,其中b∈R.
,其中b∈R.
(Ⅰ)f(x)在x=-1处的切线与x轴平行,求b的值;
(Ⅱ)求f(x)的单调区间.
解:(Ⅰ)由题意f(x)=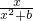 ,故f′(x)=
,故f′(x)=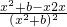 =
=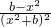 …(2分)
…(2分)
依题意,由f′(-1)=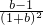 =0,得b=1.…(4分)
=0,得b=1.…(4分)
经检验,b=1符合题意.…(5分)
(Ⅱ)①当b=0时,f(x)= .
.
故f(x)的单调减区间为(-∞,0),和(0,+∞);无单调增区间. …(6分)
②当b>0时,f′(x)=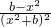 .令f′(x)=0,得x1=-
.令f′(x)=0,得x1=- ,x2=
,x2= …(8分)
…(8分)
故f(x)和f′(x)的情况如下:
故f(x)的单调减区间为(-∞,- ),(
),( ,+∞);单调增区间为(-
,+∞);单调增区间为(- ,
, ).…(11分)
).…(11分)
③当b<0时,f(x)的定义域为D={x|x≠± },因为f′(x)=
},因为f′(x)=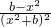 <0在D上恒成立,
<0在D上恒成立,
故f(x)的单调减区间为(-∞,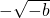 ),(
),(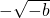 ,
, ),(
),( ,+∞);无单调增区间.…(13分)
,+∞);无单调增区间.…(13分)
分析:(Ⅰ)由题意可得由f′(-1)=0,求导数代入可得关于b的方程,解之可得;
(Ⅱ)分b=0,b>0和b<0三种情形,由导数的正负获得函数的单调区间.
点评:本题考查利用导数研究函数的单调性,以及切线问题,属中档题.
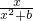 ,故f′(x)=
,故f′(x)=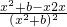 =
=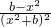 …(2分)
…(2分)依题意,由f′(-1)=
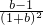 =0,得b=1.…(4分)
=0,得b=1.…(4分)经检验,b=1符合题意.…(5分)
(Ⅱ)①当b=0时,f(x)=
 .
.故f(x)的单调减区间为(-∞,0),和(0,+∞);无单调增区间. …(6分)
②当b>0时,f′(x)=
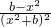 .令f′(x)=0,得x1=-
.令f′(x)=0,得x1=- ,x2=
,x2= …(8分)
…(8分)故f(x)和f′(x)的情况如下:
| x | (-∞,- ) ) | - | (- , , ) ) |  | ( ,+∞) ,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
 ),(
),( ,+∞);单调增区间为(-
,+∞);单调增区间为(- ,
, ).…(11分)
).…(11分)③当b<0时,f(x)的定义域为D={x|x≠±
 },因为f′(x)=
},因为f′(x)=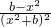 <0在D上恒成立,
<0在D上恒成立,故f(x)的单调减区间为(-∞,
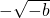 ),(
),(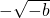 ,
, ),(
),( ,+∞);无单调增区间.…(13分)
,+∞);无单调增区间.…(13分)分析:(Ⅰ)由题意可得由f′(-1)=0,求导数代入可得关于b的方程,解之可得;
(Ⅱ)分b=0,b>0和b<0三种情形,由导数的正负获得函数的单调区间.
点评:本题考查利用导数研究函数的单调性,以及切线问题,属中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|