题目内容
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=
.
(I)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A-BE-P的大小.
| 3 |
(I)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A-BE-P的大小.


证明:(I)如图所示,连接BD,由ABCD是菱形且∠BCD=60°知,
△BCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,所以BE⊥AB,
又因为PA⊥平面ABCD,BE?平面ABCD,
所以PA⊥BE,而PA∩AB=A,因此 BE⊥平面PAB.
又BE?平面PBE,所以平面PBE⊥平面PAB.
(II)由(I)知,BE⊥平面PAB,PB?平面PAB,所以PB⊥BE.
又AB⊥BE,所以∠PBA是二面角A-BE-P的平面角.
在Rt△PAB中,tan∠PBA=
| PA |
| AB |
| 3 |
故二面角A-BE-P的大小为60°.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.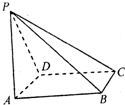 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,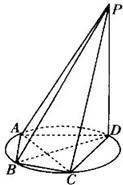 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.