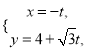Question

【题目】已知圆内接四边形ABCD的边

（Ⅰ）求角C的大小和BD的长；

（Ⅱ）求四边形ABCD的面积及外接圆的半径.

Answer 1

【答案】(Ⅰ) ； (Ⅱ) 面积； 外接圆半径为

【解析】

试题（1）连结BD，由于A+C=180°，则，在中，和在中分别应用余弦定理即可求得BD和角C；
（2）由于A+C=180°，则sinA=sinC，由四边形ABCD的面积为S△ABD+S△BCD，应用面积公式可得面积，再由正弦定理，得到边与角的比值，即为外接圆的半径．

试题解析：

(1)如图，连结BD，由于，所以。

由题设及余弦定理得

在中，①

在中，②

由①②得=，

解得，

又，

故

则。

(2) 因为，所以。

∴四边形ABCD的面积。

由正弦定理可得四边形ABCD的外接圆半径。