题目内容
如图,量角器外缘边上有A,P,Q三点,它们所表示的读数分别是180°,70°,30°,则∠PAQ的大小为 【 】
| A.10° | B.20° | C.30° | D.40° |
B
解析试题分析:
解:P、Q所表示的读数分别是70°,30°,则设圆心是O,连接OP,OQ,则∠POQ=40°,∠PAQ与∠POQ是同弧所对的圆心角与圆周角,因而∠PAQ= ∠POQ=20度.故选B
∠POQ=20度.故选B
考点:
点评:能够把量角器问题抽象为圆的问题,利用圆的知识来解决,是数学知识与实际相联系考查了运用能力。

练习册系列答案
相关题目
若 ,则tan
,则tan =
=
A. | B. | C. | D. |
若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数为 ( )
A. | B.2 | C. | D. |
若 为角
为角 终边上一点,则
终边上一点,则 ( )
( )
A. | B. | C. | D. |
函数y=2sin(-2x+ )的单调减区间为( )
)的单调减区间为( )
A. | B. |
C. | D. |
若函数 是偶函数,则
是偶函数,则 的值可以是( )
的值可以是( )
A. | B. | C. | D. |
设函数
 的最小正周期为
的最小正周期为 ,且
,且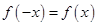 ,则( )
,则( )
A. 在 在 单调递减 单调递减 | B. 在 在 单调递减 单调递减 |
C. 在 在 单调递增 单调递增 | D. 在 在 单调递增 单调递增 |
由y=f(x)的图象向左平移 个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到y=2sin
个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到y=2sin 的图象,则 f(x)为
的图象,则 f(x)为
A.2sin | B.2sin | C.2sin | D.2sin |
 )+
)+ 是奇函数,且在[0,
是奇函数,且在[0, 上是减函数的
上是减函数的


