题目内容
函数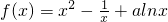 在(1,2)上存在单调递增区间的充要条件是________.
在(1,2)上存在单调递增区间的充要条件是________.
a∈(- ,+∞)
,+∞)
分析:先将函数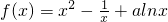 在(1,2)上存在单调递增区间的问题转化为其导函数f′(x)>0在(1,2)上能成立问题,再将导函数的分子看做新函数g(x),通过导数讨论其图象性质即可得g(x)>0在(1,2)上能成立时a的范围
在(1,2)上存在单调递增区间的问题转化为其导函数f′(x)>0在(1,2)上能成立问题,再将导函数的分子看做新函数g(x),通过导数讨论其图象性质即可得g(x)>0在(1,2)上能成立时a的范围
解答: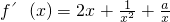 =
= (x>0)
(x>0)
设g(x)=2x3+ax+1,则g′(x)=6x2+a
若a≥-6,则因为6x2>6在(1,2)上恒成立,所以g′(x)>0,从而f′(x)>0,f(x)在(1,2)上为增函数
若-24<a<-6,则由g′(x)=0,得x=±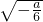 且2>
且2>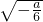 >1
>1
∴g(x)在(1,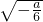 )上是减函数,在(
)上是减函数,在(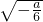 ,2)上为增函数
,2)上为增函数
要使函数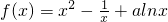 在(1,2)上存在单调递增区间
在(1,2)上存在单调递增区间
只需g(x)>0在(1,2)上能成立
只需g(1)=3+a>0,或g(2)=17+2a>0
即a>- ,此时-
,此时- <a<-6
<a<-6
若a≤-24,则因为24>6x2>6在(1,2)上恒成立,所以g′(x)<0,从而f′(x)<0,f(x)在(1,2)上为减函数,不合题意
综上所述,函数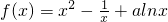 在(1,2)上存在单调递增区间的充要条件是a∈(-
在(1,2)上存在单调递增区间的充要条件是a∈(- ,+∞)
,+∞)
故答案为a∈(- ,+∞)
,+∞)
点评:本题考查了导数运算和导数在函数单调性中的应用,不等式能成立问题的解法,分类讨论的思想方法和转化化归的思想方法,确定讨论标准并不重不漏是解决本题的关键
 ,+∞)
,+∞)分析:先将函数
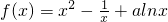 在(1,2)上存在单调递增区间的问题转化为其导函数f′(x)>0在(1,2)上能成立问题,再将导函数的分子看做新函数g(x),通过导数讨论其图象性质即可得g(x)>0在(1,2)上能成立时a的范围
在(1,2)上存在单调递增区间的问题转化为其导函数f′(x)>0在(1,2)上能成立问题,再将导函数的分子看做新函数g(x),通过导数讨论其图象性质即可得g(x)>0在(1,2)上能成立时a的范围解答:
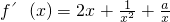 =
= (x>0)
(x>0)设g(x)=2x3+ax+1,则g′(x)=6x2+a
若a≥-6,则因为6x2>6在(1,2)上恒成立,所以g′(x)>0,从而f′(x)>0,f(x)在(1,2)上为增函数
若-24<a<-6,则由g′(x)=0,得x=±
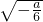 且2>
且2>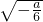 >1
>1∴g(x)在(1,
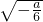 )上是减函数,在(
)上是减函数,在(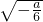 ,2)上为增函数
,2)上为增函数要使函数
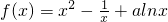 在(1,2)上存在单调递增区间
在(1,2)上存在单调递增区间只需g(x)>0在(1,2)上能成立
只需g(1)=3+a>0,或g(2)=17+2a>0
即a>-
 ,此时-
,此时- <a<-6
<a<-6若a≤-24,则因为24>6x2>6在(1,2)上恒成立,所以g′(x)<0,从而f′(x)<0,f(x)在(1,2)上为减函数,不合题意
综上所述,函数
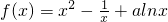 在(1,2)上存在单调递增区间的充要条件是a∈(-
在(1,2)上存在单调递增区间的充要条件是a∈(- ,+∞)
,+∞)故答案为a∈(-
 ,+∞)
,+∞)点评:本题考查了导数运算和导数在函数单调性中的应用,不等式能成立问题的解法,分类讨论的思想方法和转化化归的思想方法,确定讨论标准并不重不漏是解决本题的关键

练习册系列答案
相关题目