题目内容
在xOy平面上给定曲线y2=2x.设点A坐标为(a,0),a∈R.求曲线上的点到点A距离的最小值d,并写出d=f(a)的函数表达式.解:设M为曲线y2=2x上的一点,则|MA|2=(x-a)2+y2=(x-a)2+2x=x2-2(a-1)x+a2=[x-(a-1)]2+(2a-1). ①
由于曲线y2=2x限定x≥0,对于①式,顶点的横坐标x=a-1,由此作如下讨论:
(1)a≥1时,当x=a-1时函数有最小值,
|MA|min2=2a-1,即d=![]() .
.
(2)a<1时,①式作为x的函数在区间[0,+∞)上单调递增,故其最小值在x=0处达到,此时|MA|min2=[0-(a-1)]2+2a-1=a2,即d=|a|.
综上所述,有d=f(a)=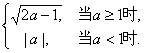

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 11、如图所示,一质点P(x,y)在xOy平面上沿曲线运动,速度大小不变,其在x轴上的投影点Q(x,0)的运动速度V=V(t)的图象大致为( )
11、如图所示,一质点P(x,y)在xOy平面上沿曲线运动,速度大小不变,其在x轴上的投影点Q(x,0)的运动速度V=V(t)的图象大致为( )













