题目内容
已知函数
.
（1）证明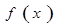
在
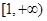上是减函数;
（2）当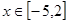
时，求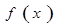的最大值和最小值.
【答案】
（1）见解析.（2）在x=1处取得最大值1，在x=-5处取得最小值－35,.
【解析】本试题主要考查了函数单调性和最值的运用。第一问中，利用定义法或者导数法可以判定单调性，得到
在
上是减函数（2）中利用第一问中的结论，结合单调性可知函数的最大值和最小值分别在x=1,x=-5处取得。
解：（1）方法一、定义法略
方法二、导数法
因为
可见函数在上是减函数;命题得证。
（2）由（1）可知
，函数先增后减，并且在x=1处取得最大值，因此f(1)=1，在x=-5处取得最小值为f(-5)=-35,故可知最小值为-35，最大值为1
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
已知函数f(x)=
+
的定义域是（ ）
| 1-x2 |
| x2-1 |
| A、[-1，1] |
| B、{-1，1} |
| C、（-1，1） |
| D、（-∞，-1]∪[1，+∞） |