题目内容
在伸缩变换下,椭圆能否变成圆?抛物线和双曲线能变成什么曲线?
探究:圆锥曲线之间的图象关系.在一定的伸缩变换规律下椭圆能够变成圆,而双曲线与抛物线仍然是双曲线和抛物线.
如:能把椭圆
=1变为中心在原点的单位圆吗?
先经过平移变换
把椭圆变为
=1,再通过伸缩变换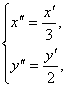
把此椭圆
变为单位圆x″2+y″2=1.上述两种变换可合成一个变换为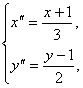
.
按照这个道理,按照变换
对于双曲线和抛物线的方程,不管进行什么样的伸缩变换（当然,把图象伸缩的无限大,或者无限小的极限位置排除在外）之后,方程特点仍然没有变,抛物线方程的二次项和一次项都没有变,双曲线的两个二次项仍然是二次项,这两个二次项之间的减号也没有变;从另外一个角度来说,把它们的图象进行压缩时,图象特点是没有变的,压缩后的图象仍然是抛物线型和双曲线型的,所以它们的图象是没有变化的,仍然是双曲线和抛物线.
练习册系列答案
阅读快车系列答案
相关题目