题目内容
(1)已知:tanα=-
,求
的值;
(2)已知α∈(0,
),β∈(
,π)sinβ=
,sin(α+β)=
,求cosα的值.
| 4 |
| 3 |
| sinα-3cosα |
| sinα+cosα |
(2)已知α∈(0,
| π |
| 2 |
| π |
| 2 |
2
| ||
| 3 |
| 7 |
| 9 |
(1)∵tanα=-
,
∴
=
=
=13;
(2)∵β∈(
,π),sinβ=
,
∴cosβ=-
=-
,
∵α∈(0,
),β∈(
,π),
∴α+β∈(
,
),
∵sin(α+β)=
,
∴cos(α+β)=-
=-
,
∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=-
×(-
)+
×
=
.
| 4 |
| 3 |
∴
| sinα-3cosα |
| sinα+cosα |
| tanα-3 |
| tanα+1 |
-
| ||
-
|
(2)∵β∈(
| π |
| 2 |
2
| ||
| 3 |
∴cosβ=-
| 1-sin2β |
| 1 |
| 3 |
∵α∈(0,
| π |
| 2 |
| π |
| 2 |
∴α+β∈(
| π |
| 2 |
| 3π |
| 2 |
∵sin(α+β)=
| 7 |
| 9 |
∴cos(α+β)=-
| 1-sin2(α+β) |
4
| ||
| 9 |
∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=-
4
| ||
| 9 |
| 1 |
| 3 |
| 7 |
| 9 |
2
| ||
| 3 |
2
| ||
| 3 |

练习册系列答案
相关题目
 ,求
,求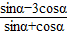 的值;
的值;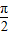 ),
),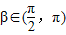 sin
sin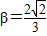 ,sin(α+β)=
,sin(α+β)= ,求cosα的值.
,求cosα的值.