题目内容
(文科)在数列{an}中,a1=1,an+1=2an+n,n∈N*.
(1)记bn=an+n+1,求证:数列{bn}是等比数列,并写出数列{an}的通项公式;
(2)在(1)的条件下,记cn=
,数列{cn}的前n项和为Sn.求证:Sn<
.
(1)记bn=an+n+1,求证:数列{bn}是等比数列,并写出数列{an}的通项公式;
(2)在(1)的条件下,记cn=
| 2n+2 |
| 2bn+3 |
| n+1 |
| 3 |
分析:(1)由已知,得出an+1+(n+2)=2an+n+n+2=2[an+(n+1)],bn+1=2bn,判断出{bn}是等比数列,通项公式易求.
(2)由(1)可知:cn=
=
=
+
<
+
,利用分组求和以及公式法求和计算出Sn再与不等式右边比较,进行证明.
(2)由(1)可知:cn=
| 2n+2 |
| 3•2n+3 |
| ||
| 3×2n+3 |
| 1 |
| 3 |
| 1 |
| 3×2n+3 |
| 1 |
| 3 |
| 1 |
| 3×2n |
解答:解:(1)∵an+1=2an+n,
∴an+1+(n+2)=2an+n+n+2=2[an+(n+1)]
即bn+1=2bn,n∈N*,
∴{bn}是等比数列且首项为b1=a1+1+1=3,公比为2,
∴bn=3•2n-1
∴an=bn-(n-1)=3×2n-1-n-1.
(2)由(1)可知:cn=
=
=
+
<
+
∴Sn<
+
=
+
(1-
)<
+
=
故Sn<
(n∈N*)
∴an+1+(n+2)=2an+n+n+2=2[an+(n+1)]
即bn+1=2bn,n∈N*,
∴{bn}是等比数列且首项为b1=a1+1+1=3,公比为2,
∴bn=3•2n-1
∴an=bn-(n-1)=3×2n-1-n-1.
(2)由(1)可知:cn=
| 2n+2 |
| 3•2n+3 |
| ||
| 3×2n+3 |
| 1 |
| 3 |
| 1 |
| 3×2n+3 |
| 1 |
| 3 |
| 1 |
| 3×2n |
∴Sn<
| n |
| 3 |
| ||||
1-
|
| n |
| 3 |
| 1 |
| 3 |
| 1 |
| 2n |
| n |
| 3 |
| 1 |
| 3 |
| n+1 |
| 3 |
故Sn<
| n+1 |
| 3 |
点评:本题考查等比数列的判定,通项公式求解,数列求和.考查转化、变形构造、计算、论证等能力.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
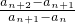 =p(p为非零常数),则称数列{an}为“等差比”数列,p叫数列
=p(p为非零常数),则称数列{an}为“等差比”数列,p叫数列 =p(p为非零常数),则称数列{an}为“等差比”数列,p叫数列
=p(p为非零常数),则称数列{an}为“等差比”数列,p叫数列