Question

（本小题满分10分）选修4-1：几何证明选讲

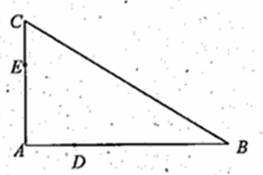如图，D，E分别为的边AB，AC上的点，且不与的顶点重合．已知AE的长为m，AC的长为n，AD，AB的长是关于x的方程的两个根．

（I）证明：C，B，D，E四点共圆；

（II）若，且求C，B，D，E所在圆的半径．

Answer 1

解：

（I）连接DE，根据题意在△ADE和△ACB中，

       AD×AB=mn=AE×AC，                     

       即.又∠DAE=∠CAB，从而△ADE∽△ACB    

       因此∠ADE=∠ACB                                 

       所以C，B，D，E四点共圆．

       （Ⅱ）m=4， n=6时，方程x²-14x+mn=0的两根为x₁=2，x₂=12.

故  AD=2，AB=12.

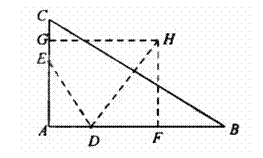
取CE的中点G，DB的中点F，分别过G，F作AC，AB的垂线，两垂线相交于H点，连接DH.因为C，B，D，E四点共圆，所以C，B，D，E四点所在圆的圆心为H，半径为DH.

由于∠A=90⁰，故GH∥AB， HF∥AC. HF=AG=5，DF= (12-2)=5.

故C，B，D，E四点所在圆的半径为5