题目内容
已知函数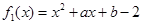 ,
,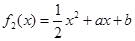 ,用
,用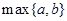 表示
表示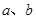 中的较大者,若
中的较大者,若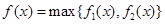 ,且
,且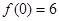 ,
,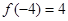 .
.
(Ⅰ)求实数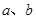 的值及函数
的值及函数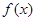 的解析式;
的解析式;
(Ⅱ)已知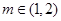 ,若
,若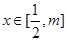 时,不等式
时,不等式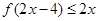 恒成立,求
恒成立,求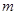 的最大值.
的最大值.
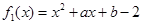 ,
,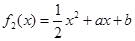 ,用
,用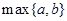 表示
表示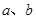 中的较大者,若
中的较大者,若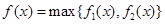 ,且
,且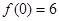 ,
,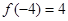 .
.(Ⅰ)求实数
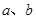 的值及函数
的值及函数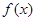 的解析式;
的解析式;(Ⅱ)已知
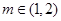 ,若
,若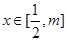 时,不等式
时,不等式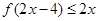 恒成立,求
恒成立,求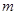 的最大值.
的最大值.(Ⅰ)由题意有: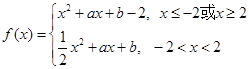 , ……………2分
, ……………2分
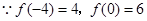 ,
,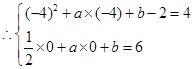 ,解得
,解得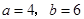 ,
,
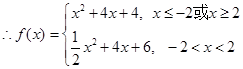 . ……………6分
. ……………6分
(Ⅱ)由(Ⅰ)得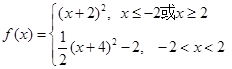 ,
,
解法一: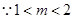 ,
,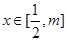 ,
,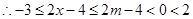 , ……8分
, ……8分
当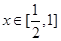 时,
时,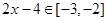 ,
,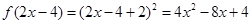 ,
,
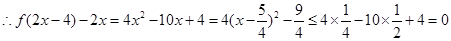 恒成立,
恒成立,
即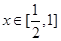 时,
时,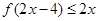 恒成立, ……………10分
恒成立, ……………10分
当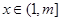 时,
时,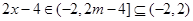 ,
,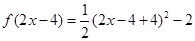
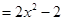 ,
,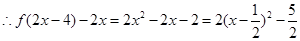 ,
,
要使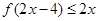 对
对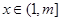 恒成立,则须
恒成立,则须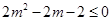 ,即
,即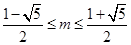
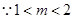 ,
,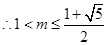 ,
,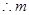 的最大值为
的最大值为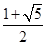 . ……………12分
. ……………12分
解法二: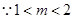 ,
,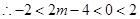 ,
,
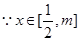 时,
时,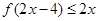 恒成立,
恒成立,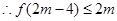 ,
,
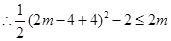 ,可得:
,可得: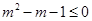 ,
,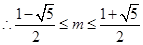 , …9分
, …9分
取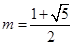 ,则
,则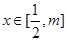 时,
时,
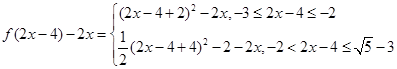

恒有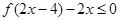 ,
,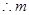 的最大值为
的最大值为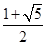 .
.
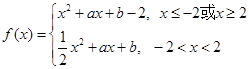 , ……………2分
, ……………2分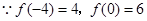 ,
,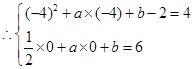 ,解得
,解得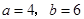 ,
,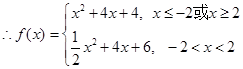 . ……………6分
. ……………6分(Ⅱ)由(Ⅰ)得
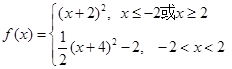 ,
,解法一:
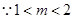 ,
,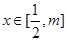 ,
,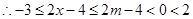 , ……8分
, ……8分当
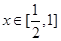 时,
时,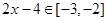 ,
,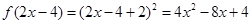 ,
,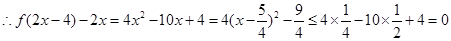 恒成立,
恒成立,即
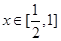 时,
时,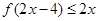 恒成立, ……………10分
恒成立, ……………10分当
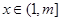 时,
时,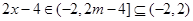 ,
,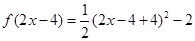
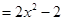 ,
,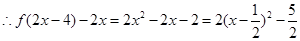 ,
,要使
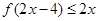 对
对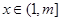 恒成立,则须
恒成立,则须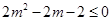 ,即
,即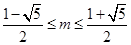
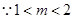 ,
,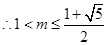 ,
,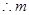 的最大值为
的最大值为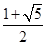 . ……………12分
. ……………12分解法二:
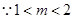 ,
,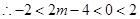 ,
,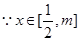 时,
时,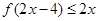 恒成立,
恒成立,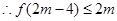 ,
,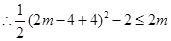 ,可得:
,可得: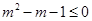 ,
,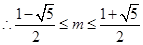 , …9分
, …9分取
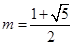 ,则
,则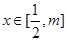 时,
时,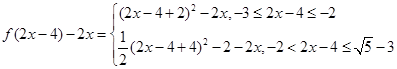

恒有
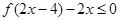 ,
,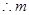 的最大值为
的最大值为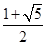 .
.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
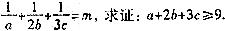
 (万件)、市场供应量
(万件)、市场供应量 (万件)与市场价格x(元/件)分别近似的满足下列关系:
(万件)与市场价格x(元/件)分别近似的满足下列关系: ,
, ,当
,当 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。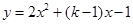 是偶函数,则( )
是偶函数,则( )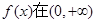 上为减函数,且
上为减函数,且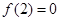 ,则不等式
,则不等式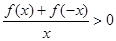 的解集为( )
的解集为( )



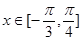 ,
,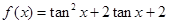 ,求
,求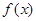 的最大值和最小值,并求出相应的
的最大值和最小值,并求出相应的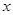 值.
值.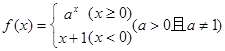 ;
;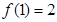 ,求
,求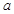 的值,并作出
的值,并作出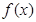 的图象;
的图象;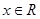 时,恒有
时,恒有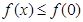 求
求
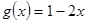 ,
, ,则
,则 ( )
( )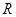 上的函数
上的函数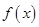 满足:
满足: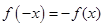 ,
, 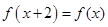 ,当且
,当且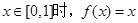 ,则
,则