题目内容
已知函数f（x）=lnx﹣2kx，（k常数）
（1）求函数f（x）的单调区间；
（2）若f（x）＜x3+lnx恒成立，求k的取值范围．
（1）求函数f（x）的单调区间；
（2）若f（x）＜x3+lnx恒成立，求k的取值范围．
解：（1）由f（x）=lnx﹣2kx，得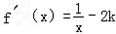
，
∵f（x）的定义域为（0，+∞），
∴当k≤0时，
，f（x）在（0，+∞）是增函数，
当k＞0时，由
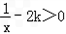，得
，
∴f（x）在（0，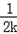
）上是增函数，在（
，+∞）上是减函数，
综上，当k≤0时，f（x）的单调增区间是（0，+∞）；
当k＞0时，f（x）的单调增区间是（0，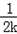
），单调减区间是（
）．
（2）由f（x）＜x3+lnx恒成立，得x3+2kx＞0恒成立，x∈（0，+∞），即2kx＞﹣x3，
∴2k＞﹣x2恒成立，
∵﹣x2＜0，2k≥0，
∴k的取值范围是[0，+∞）．
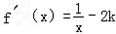，∵f（x）的定义域为（0，+∞），
∴当k≤0时，
，f（x）在（0，+∞）是增函数，当k＞0时，由
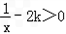，得，∴f（x）在（0，
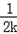）上是增函数，在（，+∞）上是减函数，综上，当k≤0时，f（x）的单调增区间是（0，+∞）；
当k＞0时，f（x）的单调增区间是（0，
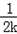），单调减区间是（）．（2）由f（x）＜x3+lnx恒成立，得x3+2kx＞0恒成立，x∈（0，+∞），即2kx＞﹣x3，
∴2k＞﹣x2恒成立，
∵﹣x2＜0，2k≥0，
∴k的取值范围是[0，+∞）．
练习册系列答案
阅读快车系列答案
相关题目