题目内容
已知函数f(x)=log2x-2log2(x+c),其中c>0.若对于任意的x∈(0,+∞),都有f(x)≤1,则c的取值范围是
- A.
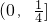
- B.
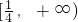
- C.

- D.

D
分析:把函数f(x)的解析式代入f(x)≤1后,利用对数式的运算性质变形,去掉对数符号后把参数c分离出来,然后利用二次函数求最值,则c的取值范围可求.
解答:由f(x)≤1,得:log2x-2log2(x+c)≤1,
整理得: ,所以x+c≥
,所以x+c≥ ,
,
即c≥ (x>0).
(x>0).
令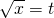 (t>0).
(t>0).
则 .
.
令g(t)= ,其对称轴为
,其对称轴为 .
.
所以 .
.
则c .
.
所以,对于任意的x∈(0,+∞),都有f(x)≤1的c的取值范围是 .
.
故选D.
点评:本题考查了对数型的函数及其应用,考查了数学转化思想,训练了利用分离变量法求参数的取值范围,解答的关键是利用对数函数的单调性去掉对数符号,是中档题.
分析:把函数f(x)的解析式代入f(x)≤1后,利用对数式的运算性质变形,去掉对数符号后把参数c分离出来,然后利用二次函数求最值,则c的取值范围可求.
解答:由f(x)≤1,得:log2x-2log2(x+c)≤1,
整理得:
 ,所以x+c≥
,所以x+c≥ ,
,即c≥
 (x>0).
(x>0).令
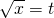 (t>0).
(t>0).则
 .
.令g(t)=
 ,其对称轴为
,其对称轴为 .
.所以
 .
.则c
 .
.所以,对于任意的x∈(0,+∞),都有f(x)≤1的c的取值范围是
 .
.故选D.
点评:本题考查了对数型的函数及其应用,考查了数学转化思想,训练了利用分离变量法求参数的取值范围,解答的关键是利用对数函数的单调性去掉对数符号,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目