题目内容
已知数列{an}满足an=2an-1+2n+1(n≥2,n∈N*),且a3=39,(1)求a1,a2.
(2)是否存在实数λ,使得数列{
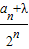 }为等差数列;若存在,求出λ的值.
}为等差数列;若存在,求出λ的值.(3)令cn=
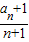 ,若cn>m对任意的n∈N*都成立,求实数m的取值范围.
,若cn>m对任意的n∈N*都成立,求实数m的取值范围.
【答案】分析:(1)由已知代入an=2an-1+2n+1(n≥2,n∈N*),且a3=39,即可求出a1,a2.
(2)假设存在实数λ,使得数列{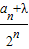 }为等差数列,求出λ的值为1,再证明数列{
}为等差数列,求出λ的值为1,再证明数列{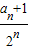 }为等差数列即可.
}为等差数列即可.
(3)由(2)得到cn=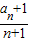 =
=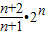 ,若cn>m对任意的n∈N*都成立,只需m小于数列{cn}的最小项,即可得到实数m的取值范围.
,若cn>m对任意的n∈N*都成立,只需m小于数列{cn}的最小项,即可得到实数m的取值范围.
解答:解:(1)由于数列{an}满足an=2an-1+2n+1(n≥2,n∈N*),且a3=39,
则a3=2a2+23+1,a2=2a1+22+1,故a2=15,a1=5;
(2)若存在实数λ,使得数列{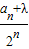 }为等差数列,
}为等差数列,
则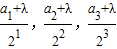 也为等差数列,
也为等差数列,
故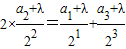
解得λ=1,
由于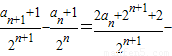
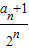 =1
=1
所以数列{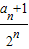 }为等差数列,首项为
}为等差数列,首项为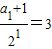 ,
,
故当λ=1时,数列{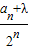 }为等差数列;
}为等差数列;
(3)由(2)知,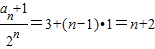
若令cn=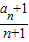 ,则cn=
,则cn=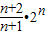
由于cn≥cn+1等价于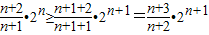
即n2+4n+2=(n+2)2-2≤0无解,故恒有cn≥cn-1
若cn>m对任意的n∈N*都成立,则必有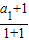 =3=c1>m
=3=c1>m
则实数m的取值范围为m<3.
点评:本题主要考查了数列的递推关系,以及等比数列求和公式,同时考查了分类讨论的数学思想,该题有一定的难度.
(2)假设存在实数λ,使得数列{
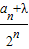 }为等差数列,求出λ的值为1,再证明数列{
}为等差数列,求出λ的值为1,再证明数列{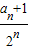 }为等差数列即可.
}为等差数列即可.(3)由(2)得到cn=
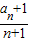 =
=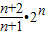 ,若cn>m对任意的n∈N*都成立,只需m小于数列{cn}的最小项,即可得到实数m的取值范围.
,若cn>m对任意的n∈N*都成立,只需m小于数列{cn}的最小项,即可得到实数m的取值范围.解答:解:(1)由于数列{an}满足an=2an-1+2n+1(n≥2,n∈N*),且a3=39,
则a3=2a2+23+1,a2=2a1+22+1,故a2=15,a1=5;
(2)若存在实数λ,使得数列{
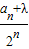 }为等差数列,
}为等差数列,则
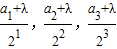 也为等差数列,
也为等差数列,故
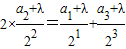
解得λ=1,
由于
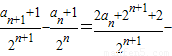
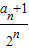 =1
=1所以数列{
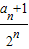 }为等差数列,首项为
}为等差数列,首项为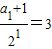 ,
,故当λ=1时,数列{
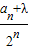 }为等差数列;
}为等差数列;(3)由(2)知,
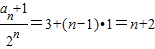
若令cn=
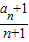 ,则cn=
,则cn=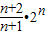
由于cn≥cn+1等价于
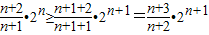
即n2+4n+2=(n+2)2-2≤0无解,故恒有cn≥cn-1
若cn>m对任意的n∈N*都成立,则必有
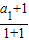 =3=c1>m
=3=c1>m则实数m的取值范围为m<3.
点评:本题主要考查了数列的递推关系,以及等比数列求和公式,同时考查了分类讨论的数学思想,该题有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目