Question

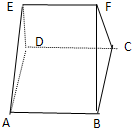如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，EF=

3

2

，EF与面AC的距离为2，则该多面体的体积为（　　）

• A、

  9

  2

• B、5
• C、6
• D、

  15

  2

Answer 1

分析：由已知中多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF与面AC的距离为2，我们易求出四棱锥E-ABCD的体积，然后根据整个几何体大于部分几何体的体积，分析已知中的四个答案，利用排除法，得到答案．

解答：解：
法一：如下图所示，连接BE、CE
则四棱锥E-ABCD的体积V_E-ABCD=

1

3

×3×3×2=6，
又∵整个几何体大于四棱锥E-ABCD的体积，
∴所求几何体的体积V_求＞V_E-ABCD，
法二：分别取AB、CD的中点G、H连EG，GH，EH，把该多面体分割成一个四棱锥与一个三棱柱，
可求得四棱锥的体积为3，三棱柱的体积

9

2

，整个多面体的体积为

15

2

．
故选D．

点评：本题考查的知识点是棱柱、棱锥、棱台的体积，其中根据根据整个几何体大于部分几何体的体积，求出四棱锥E-ABCD的体积，并与已知中的四个答案进行比较，利用排除法是解答此类问题的捷径．