题目内容
数列{an}的通项公式为
，若数列{an}是个递增数列，则a的范围是
- A.a＜2
- B.a≥1
- C.
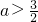
- D.a＜3
D
分析：由已知数列{an}是个递增数列，可得an+1-an＞0对于任意的正整数n都成立，解出即可．
解答：∵数列{an}是个递增数列，∴an+1-an＞0，对于任意的正整数n都成立，
∵an+1-an=（n+1）2-a（n+1）+2-（n2-an+2）=2n+1-a，
∴2n+1-a＞0，对于任意的正整数n都成立，
∴a＜（2n+1）min=2×1+1=3．
故选D．
点评：正确理解数列{an}是个递增数列的意义是解题的关键．
分析：由已知数列{an}是个递增数列，可得an+1-an＞0对于任意的正整数n都成立，解出即可．
解答：∵数列{an}是个递增数列，∴an+1-an＞0，对于任意的正整数n都成立，
∵an+1-an=（n+1）2-a（n+1）+2-（n2-an+2）=2n+1-a，
∴2n+1-a＞0，对于任意的正整数n都成立，
∴a＜（2n+1）min=2×1+1=3．
故选D．
点评：正确理解数列{an}是个递增数列的意义是解题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
，Tn为数列{bn}的前n项和，求Tn．