题目内容
已知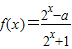 (a∈R)是奇函数.
(a∈R)是奇函数.(1)求a的值;
(2)求函数F(x)=f(x)+2x-
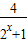 -1的零点;
-1的零点;(3)设g(x)=log4
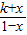 ,若方程f-1(x)=g(x)在x∈[
,若方程f-1(x)=g(x)在x∈[ ,
, ]上有解,求实数k的取值范围.
]上有解,求实数k的取值范围.
【答案】分析:(1)由题意可得:f(0)=0,解得a=1,注意验证;
(2)把(1)的结论代入可得函数,转化为方程的根可得答案;
(3)求函数的反函数可得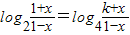 ,由对数的运算性质可得
,由对数的运算性质可得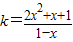 ,用换元法令m=1-x,由关于m的函数的范围可得答案.
,用换元法令m=1-x,由关于m的函数的范围可得答案.
解答:解:(1)由奇函数的定义可得:f(-x)=-f(x),
取x=0即得f(0)=0,解得a=1,2分
经验证知当a=1时,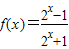 ,此时满足f(x)=-f(-x),
,此时满足f(x)=-f(-x),
故当a=1时,f(x)在R上的奇函数,4分
(2)由(1)知: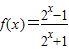 ,故F(x)=
,故F(x)=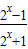 +
+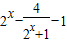 =
=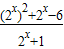 6分
6分
由(2x)2+2x-6=0,可得2x=2,8分
所以x=1,即F(x)的零点为x=1. 10分
(3)由f-1(x)=g(x)得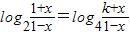 ,11分
,11分
由对数函数的运算性质可得: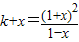 12分
12分
显然当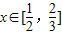 时k+x>0,即
时k+x>0,即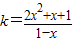 13分
13分
设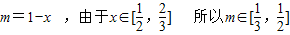 14分
14分
于是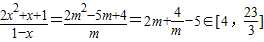 15分
15分
所以实数k的取值范围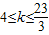 16分.
16分.
点评:本题考查函数的奇偶性和零点,涉及对数的运算,属中档题.
(2)把(1)的结论代入可得函数,转化为方程的根可得答案;
(3)求函数的反函数可得
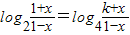 ,由对数的运算性质可得
,由对数的运算性质可得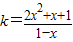 ,用换元法令m=1-x,由关于m的函数的范围可得答案.
,用换元法令m=1-x,由关于m的函数的范围可得答案.解答:解:(1)由奇函数的定义可得:f(-x)=-f(x),
取x=0即得f(0)=0,解得a=1,2分
经验证知当a=1时,
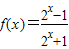 ,此时满足f(x)=-f(-x),
,此时满足f(x)=-f(-x),故当a=1时,f(x)在R上的奇函数,4分
(2)由(1)知:
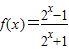 ,故F(x)=
,故F(x)=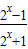 +
+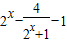 =
=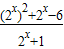 6分
6分由(2x)2+2x-6=0,可得2x=2,8分
所以x=1,即F(x)的零点为x=1. 10分
(3)由f-1(x)=g(x)得
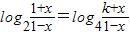 ,11分
,11分由对数函数的运算性质可得:
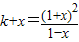 12分
12分显然当
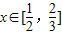 时k+x>0,即
时k+x>0,即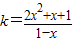 13分
13分设
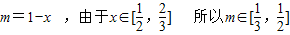 14分
14分于是
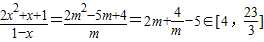 15分
15分所以实数k的取值范围
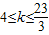 16分.
16分.点评:本题考查函数的奇偶性和零点,涉及对数的运算,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
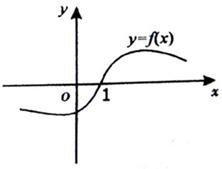 已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论:
已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论: ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)