题目内容
已知曲线C: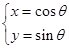 (
(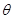 为参数).
为参数).
(1)将C的参数方程化为普通方程;
(2)若把C上各点的坐标经过伸缩变换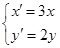 后得到曲线
后得到曲线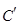 ,求曲线
,求曲线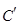 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
⑴ 的普通方程为
的普通方程为 .⑵曲线
.⑵曲线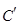 上任意一点到两坐标轴距离之积的最大值为3.
上任意一点到两坐标轴距离之积的最大值为3.
解析试题分析:⑴ 的普通方程为
的普通方程为 . (4分)
. (4分)
⑵(方法一) 经过伸缩变换
经过伸缩变换 后,
后, (
(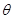 为参数), (7分)
为参数), (7分)
∴ ≤3,当
≤3,当 时取得“=”.
时取得“=”.
∴曲线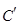 上任意一点到两坐标轴距离之积的最大值为3. (10分)
上任意一点到两坐标轴距离之积的最大值为3. (10分)
(方法二)  经过伸缩变换
经过伸缩变换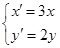 后,
后, ,∴
,∴ . (7分)
. (7分)
∵ ≥
≥ ,∴
,∴ ≤3.
≤3.
当且仅当 时取“=”.
时取“=”.
∴曲线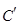 上任意一点到两坐标轴距离之积的最大值为3. (10分)
上任意一点到两坐标轴距离之积的最大值为3. (10分)
考点:本题主要考查参数方程,曲线的伸缩变换,基本不等式的应用。
点评:容易题,所涉及的公式要牢记,应用基本不等式确定最值,体现解题的灵活性。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出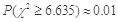 ,则下列说法正确的( )
,则下列说法正确的( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4)(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2)(13,1),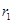 表示变量Y与X之间的线性相关系数,
表示变量Y与X之间的线性相关系数,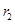 表示变量V与U之间的线性相关系数,则( )
表示变量V与U之间的线性相关系数,则( )
A.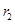 < <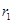 <0 <0 | B.0<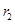 < <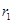 | C.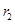 <0< <0<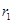 | D.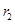 = =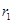 |
已知某高中高一800名学生某次考试的数学成绩,现在想知道不低于120分,90~
120分,75~90分,60~75分,60分以下的学生分别占多少,需要做的工作是( )
| A.抽取样本,据样本估计总体 | B.求平均成绩 |
| C.进行频率分布 | D.计算方差 |
 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点
为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点 为极点,
为极点, 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线 的方程为
的方程为 .
. ,求
,求 的值.
的值.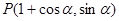 ,参数
,参数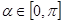
 ,点Q在曲线C:
,点Q在曲线C: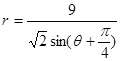 上.
上.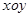 中,直线
中,直线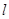 的参数方程为
的参数方程为 (t为参数,α为直线
(t为参数,α为直线 .
.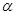 的值;
的值; 直线
直线 的值.
的值.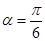 .
.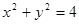 相交于两点A,B,求点P到A,B两点的距离之积.
相交于两点A,B,求点P到A,B两点的距离之积.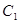 的极坐标方程是
的极坐标方程是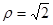 ,曲线
,曲线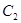 的参数方程是
的参数方程是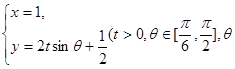 是参数).
是参数). 的取值范围,使得
的取值范围,使得