题目内容
(本小题共13分)已知椭圆 的右焦点为
的右焦点为 ,
,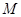 为椭圆的上顶点,
为椭圆的上顶点, 为坐标原点,且△
为坐标原点,且△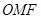 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点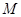 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于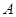 ,
,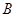 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为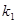 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点(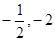 ).
).
解:(Ⅰ)由△ 是等腰直角三角形,得
是等腰直角三角形,得 ,
, ,
,
故椭圆方程为 .
…………5分
.
…………5分
(Ⅱ)若直线 的斜率存在,设
的斜率存在,设 方程为
方程为 ,依题意
,依题意 .
.
设 ,
, ,
,
由  得
得  . ………7分
. ………7分
则 .
.
由已知 ,
,
所以 ,
,
即 .
………10分
.
………10分
所以 ,整理得
,整理得  .
.
故直线 的方程为
的方程为 ,即
,即 (
( )
) .
.
所以直线 过定点(
过定点( ).
………12分
).
………12分
若直线 的斜率不存在,设
的斜率不存在,设 方程为
方程为 ,
,
设 ,
, ,
,
由已知 ,
,
得 .此时
.此时 方程为
方程为 ,显然过点(
,显然过点( ).
).
综上,直线 过定点(
过定点( ).
………13分
).
………13分
【解析】本题考查椭圆的方程和直线与椭圆的相交问题,考查学生利用待定系数法和解析法的解题能力.
待定系数法:如果题目给出是何曲线,可根据题目条件,恰当的设出曲线方程,然后借助条件进一步确定 求椭圆的标准方程应从“定形”“定式”“定量”三个方面去思考。“定形”是指对称中心在原点,焦点在哪条对称轴上;“定式”是指根据“形”设出相应的椭圆方程的具体形式;“定量”是指利用定义法或待定系数法确定
求椭圆的标准方程应从“定形”“定式”“定量”三个方面去思考。“定形”是指对称中心在原点,焦点在哪条对称轴上;“定式”是指根据“形”设出相应的椭圆方程的具体形式;“定量”是指利用定义法或待定系数法确定 的值.本题第一问利用椭圆的离心率和直线与椭圆相切判别式为0得到两个等式求解
的值.本题第一问利用椭圆的离心率和直线与椭圆相切判别式为0得到两个等式求解 的值;关于直线与圆锥曲线位置关系的存在性问题,一般先假设存在满足题意的元素,经过推理论证,如果得到可以成立的结果,就可以作出存在的结论;若得到与已知条件、定义、公理、定理、性质相矛盾的量,则说明假设不成立.本题的第二问就是利用这个解题思路,借助韦达定理和距离公式进行转化和探索.
的值;关于直线与圆锥曲线位置关系的存在性问题,一般先假设存在满足题意的元素,经过推理论证,如果得到可以成立的结果,就可以作出存在的结论;若得到与已知条件、定义、公理、定理、性质相矛盾的量,则说明假设不成立.本题的第二问就是利用这个解题思路,借助韦达定理和距离公式进行转化和探索.

 。
。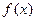 的最小正周期:
的最小正周期: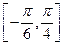 上的最大值和最小值。
上的最大值和最小值。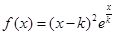 。
。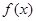 的单调区间;
的单调区间; ,都有
,都有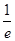 ,求
,求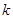 的取值范围。
的取值范围。 :
: ,其中等于
,其中等于 的项有
的项有 个
个 ,
,
 ,
,
 .
. ,求
,求 ;
; ,求函数
,求函数 的最小值.
的最小值. ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间.