题目内容
设函数 ,曲线
,曲线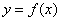 在点
在点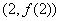 处的切线方程为
处的切线方程为 .
.
(1)求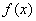 的解析式;
的解析式;
(2)证明:曲线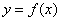 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
解:(1)方程 可化为
可化为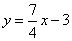 .
.
当 时,
时, . 又
. 又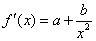
于是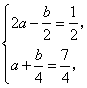 解得
解得 ,故
,故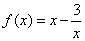 .
.
(2)设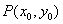 为曲线上任一点,由
为曲线上任一点,由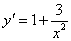 知曲线在点
知曲线在点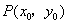 处的切线方程为
处的切线方程为
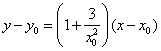 ,即
,即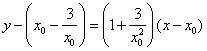 .
.
令 得
得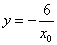 ,从而得切线与直线
,从而得切线与直线 的交点坐标为
的交点坐标为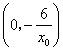 .
.
令 得
得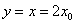 ,
,
从而得切线与直线 的交点坐标为
的交点坐标为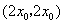 .
.
所以点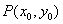 处的切线与直线
处的切线与直线 ,
, 所围成的三角形面积为
所围成的三角形面积为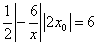 .
.
故曲线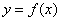 上任一点处的切线与直线
上任一点处的切线与直线 ,
, 所围成的三角形的面积为定值,此定值为
所围成的三角形的面积为定值,此定值为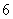

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)已知零件个数与加工时间线性相关,求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?

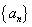 的公差
的公差 ,其前四项和为10,且
,其前四项和为10,且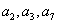 成等比数列
成等比数列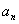
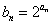 ,求数列
,求数列 的前
的前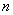 项和
项和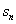
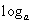 (2x2-1)的导数是( )
(2x2-1)的导数是( )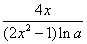 B.
B. 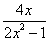 C.
C. 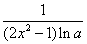 D.
D. 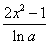
 ( )
( )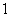 B.-
B.-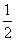 C.
C.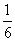 D.
D.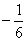
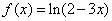 ,则
,则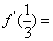
 ( )
( )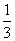 B.
B.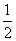 C.
C.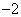 D.
D.