题目内容
如图,已知正四面ABCD中,AE=
AB,CF=
CD,则直线DE和BF所成的角的余弦值为

| 1 |
| 4 |
| 1 |
| 4 |

分析:设正四面体的棱长等于1,设向量
=
,
=
,
=
,将向量
、
表示为向量
,
,
的线性组合,利用正四面体的性质、向量的加减与数量积运算法则,算出cos<
,
>=-
,结合异面直线所成角的定义即可得出直线DE和BF所成的角的余弦值.
| DA |
| a |
| DB |
| b |
| DC |
| c |
| DE |
| BF |
| a |
| b |
| c |
| DE |
| BF |
| 4 |
| 13 |
解答:解:正四面ABCD中,设向量
=
,
=
,
=
,
则向量
,
,
两两夹角为60°,
设正四面体的棱长等于1,
则
•
=
•
=
•
=cos60°=
,
∵△ABD中,AE=
AB,
∴
=
+
=
+
,
同理由CF=
CD,可得
=
-
=-
+
,
∴
=
=
=
=
,
同理可得
=
=
,
∵
•
=(
+
)•(-
+
)=-
•
+
•
-
2+
•
=-
∴cos<
,
>=
=
=-
,
结合异面直线DE和BF所成的角为锐角或直角,
可得直线DE和BF所成的角的余弦值为-cos<
,
>=
.
故答案为:
| DA |
| a |
| DB |
| b |
| DC |
| c |
则向量
| a |
| b |
| c |
设正四面体的棱长等于1,
则
| a |
| b |
| b |
| c |
| c |
| a |
| 1 |
| 2 |
∵△ABD中,AE=
| 1 |
| 4 |
∴
| DE |
| 3 |
| 4 |
| DA |
| 1 |
| 4 |
| DB |
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
同理由CF=
| 1 |
| 4 |
| BF |
| DF |
| DB |
| b |
| 3 |
| 4 |
| c |
∴
| |DE| |
(
|
|
|
| ||
| 4 |
同理可得
| |BF| |
(-
|
| ||
| 4 |
∵
| DE |
| BF |
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
| b |
| 3 |
| 4 |
| c |
| 3 |
| 4 |
| a |
| b |
| 9 |
| 16 |
| a |
| c |
| 1 |
| 4 |
| b |
| 3 |
| 16 |
| b |
| c |
| 1 |
| 4 |
∴cos<
| DE |
| BF |
| ||||
|
-
| ||||||||
|
| 4 |
| 13 |
结合异面直线DE和BF所成的角为锐角或直角,
可得直线DE和BF所成的角的余弦值为-cos<
| DE |
| BF |
| 4 |
| 13 |
故答案为:
| 4 |
| 13 |
点评:本题在正四面体中求异面直线所成角的余弦值,着重考查了正四面体的性质、向量的加减与数量积运算、异面直线所成角的定义及其求法等知识,属于中档题.

练习册系列答案
相关题目
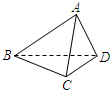 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.

