题目内容
求下列函数的值域
①y=3x+2(-1≤x≤1)②f(x)=2+
③y=
④y=x+
.
①y=3x+2(-1≤x≤1)②f(x)=2+
| 4-x |
| x |
| x+1 |
| 1 |
| x |
(1)∵一次函数f(x)=3x+2在[-1,1]上为增函数,
∴f(-1)≤y≤f(1),即-1≤y≤5
∴函数y=3x+2(-1≤x≤1)的值域为[-1,5]
(2)∵函数f(x)=2+
的定义域为(-∞,4]
且此函数在定义域上为单调减函数,
∴f(x)≥f(4)=2
∴函数f(x)=2+
的值域为[2,+∞)
(3)函数y=
=1-
由反比例函数的图象知
≠0
∴y≠1
∴函数y=
的值域为(-∞,1)∪(1,+∞)
(4)x>0时,y=x+
≥2
=2
x<0时,y=x+
=-(-x-
)≤-2
=-2
∴函数y=x+
的值域为(-∞,-2]∪[2,+∞)
∴f(-1)≤y≤f(1),即-1≤y≤5
∴函数y=3x+2(-1≤x≤1)的值域为[-1,5]
(2)∵函数f(x)=2+
| 4-x |
且此函数在定义域上为单调减函数,
∴f(x)≥f(4)=2
∴函数f(x)=2+
| 4-x |
(3)函数y=
| x |
| x+1 |
| 1 |
| x+1 |
由反比例函数的图象知
| 1 |
| x+1 |
∴y≠1
∴函数y=
| x |
| x+1 |
(4)x>0时,y=x+
| 1 |
| x |
x×
|
x<0时,y=x+
| 1 |
| x |
| 1 |
| x |
(-x)×
|
∴函数y=x+
| 1 |
| x |

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 ③
③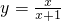 ④
④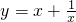 .
. ③
③ ④
④ .
.