题目内容
已知函数f(x)=1nx﹣ax.
(Ⅰ)若f(x)的最大值为1,求a的值;
(Ⅱ)设l是函数f(x)=1nx﹣ax图象上任意一点的切线,证明:函数f(x)=1nx﹣ax的图象除该点外恒在直线l的下方.
考点:
利用导数研究曲线上某点切线方程;函数在某点取得极值的条件.
专题:
压轴题;导数的综合应用.
分析:
(Ⅰ)先求出导数,对a分类讨论即可得出;
(Ⅱ)利用导数的几何意义求出切线的斜率,进而得到切线的方程g(x)=0,构造函数h(x)=g(x)﹣f(x),利用导数证明h(x)的最小值≥0即可.
解答:
解:(Ⅰ)易知,函数f(x)的定义域为(0,+∞),
∵![]() ,①当a≤0时,f′(x)≥0,∴函数f(x)单调递增,因此函数在(0,+∞)上无最大值,不符合题意,应舍去;
,①当a≤0时,f′(x)≥0,∴函数f(x)单调递增,因此函数在(0,+∞)上无最大值,不符合题意,应舍去;
②当a>0时,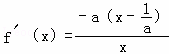 ,令f′(x)=0,则
,令f′(x)=0,则![]() .
.
当![]() 时,f′(x)>0,函数f(x)单调递增;当
时,f′(x)>0,函数f(x)单调递增;当![]() 时,f′(x)<0,函数f(x)单调递减.
时,f′(x)<0,函数f(x)单调递减.
∴当![]() 时,函数f(x)取得极大值,也即最大值.
时,函数f(x)取得极大值,也即最大值.
∴![]() =1,即
=1,即![]() ,解得
,解得![]() .
.
(Ⅱ)设P(x0,lnx0﹣ax0)是曲线f(x)=lnx﹣ax的图象上的任意一点,则过点P的切线的斜率为![]() ,
,
∴切线为![]() ,化为y=g(x)=
,化为y=g(x)=![]() ,
,
令h(x)=g(x)﹣f(x)=![]() ﹣(lnx﹣ax),
﹣(lnx﹣ax),
∴h′(x)=![]() =
=![]() ,令h′(x)=0,解得x=x0.
,令h′(x)=0,解得x=x0.
当0<x<x0时,h′(x)<0,函数h(x)单调递减;当x>x0时,h′(x)>0,函数h(x)单调递增.
因此当x=x0时,函数h(x)取得最小值,∴h(x)≥h(x0)=![]() =0,
=0,
∴g(x)≥f(x),函数f(x)=1nx﹣ax的图象除切点外恒在直线l的下方.
点评:
熟练掌握利用导数研究函数的单调性极值等性质、分类讨论的思想方法是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|