Question

若a∈Z，方程y²－xy＋ax²－5x－1=0表示两条直线，求此两条直线的夹角.

Answer 1

解法一:设此两条直线的方程分别为y＋A₁x＋C₁=0和y＋A₂x＋C₂=0.

由(y＋A₁x＋C₁)(y＋A₂x＋C₂)=0，得

y²＋(A₁＋A₂)xy＋A₁A₂x²＋(A₁C₂＋A₂C₁)x＋(C₁＋C₂)y＋C₁C₂=0.

对照方程y²－xy＋ax²－5x－1=0,知

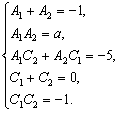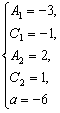解得或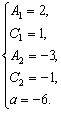

∴两直线的方程分别为y－3x－1=0和y＋2x＋1=0,其中k₁=3，k₂=－2.

设两条直线的夹角为θ，则tanθ=||=1.

∵θ∈(0°，90°］，∴θ=45°.

故此两条直线的夹角是45°.

解法二:若把y²－xy＋ax²－5x－1=0看作关于y的一元二次方程，则它的判别式Δ₁=(－x)²－4·(ax²－5x－1)=(1－4a)x²＋20x＋4应为完全平方式.

∴(1－4a)x²＋20x＋4的判别式Δ₂=20²－4·(1－4a)·4应为0.

由25－(1－4a)=0，得a=－6.

∴原方程为y²－xy－6x²－5x－1=0，

即(y＋2x)(y－3x)－5x－1=0,(y＋2x＋1)(y－3x－1)=0.

∴y＋2x＋1=0，y－3x－1=0为两直线的方程.

∴k₁=－2，k₂=3.

设两直线的夹角为θ，则tanθ=||=1.

又θ∈(0°，90°］，∴θ=45°.

故此两条直线的夹角为45°.