题目内容
已知函数f(x)=2x+a•2-|x|(a∈R)满足 .若存在x0∈[1,2]使得不等式2xf(2x)+mf(x)≥0成立,则实数m的取值范围是
.若存在x0∈[1,2]使得不等式2xf(2x)+mf(x)≥0成立,则实数m的取值范围是
- A.[-5,+∞)
- B.[-
 ,+∞)
,+∞) - C.(-∞,-17]
- D.(-∞,-15]
B
分析:先由 解出a=1得 f(x)=2x+2-|x|,代入不等式2xf(2x)+mf(x)≥0,由于存在x0∈[1,2]使不等式成立,故整理得-m≤
解出a=1得 f(x)=2x+2-|x|,代入不等式2xf(2x)+mf(x)≥0,由于存在x0∈[1,2]使不等式成立,故整理得-m≤ ,让-m小于等于
,让-m小于等于 在∈[1,2]上的最大值即可解出实数m的取值范围.
在∈[1,2]上的最大值即可解出实数m的取值范围.
解答:由题设函数f(x)=2x+a•2-|x|(a∈R)满足 .
.
得 +a×
+a× =2 ①
=2 ①
∵ >0
>0
∴①式可变为 +a×
+a×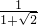 =
= +a(
+a(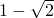 )=2
)=2
故有1+a+ (1-a)=2,a(1-
(1-a)=2,a(1- )=1-
)=1- ,解得a=1
,解得a=1
所以 f(x)=2x+2-|x|
当存在x0∈[1,2]时,使不等式2xf(2x)+mf(x)≥0恒成立,即23x+2-x+m(2x+2-x)≥0成立,
即24x+1+m(22x+1)≥0成立,即-m≤ =22x+1-2+
=22x+1-2+ ≤
≤
故m≥-
故应选B.
点评:本题考点是指数函数的综合题,考查复杂指数式的恒等变形与复杂指数方程的变形,运算量较大,由于本题最后解决的是存在性的问题,要区分开其与恒成立问题的区别.
分析:先由
 解出a=1得 f(x)=2x+2-|x|,代入不等式2xf(2x)+mf(x)≥0,由于存在x0∈[1,2]使不等式成立,故整理得-m≤
解出a=1得 f(x)=2x+2-|x|,代入不等式2xf(2x)+mf(x)≥0,由于存在x0∈[1,2]使不等式成立,故整理得-m≤ ,让-m小于等于
,让-m小于等于 在∈[1,2]上的最大值即可解出实数m的取值范围.
在∈[1,2]上的最大值即可解出实数m的取值范围.解答:由题设函数f(x)=2x+a•2-|x|(a∈R)满足
 .
.得
 +a×
+a× =2 ①
=2 ①∵
 >0
>0∴①式可变为
 +a×
+a×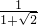 =
= +a(
+a(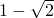 )=2
)=2故有1+a+
 (1-a)=2,a(1-
(1-a)=2,a(1- )=1-
)=1- ,解得a=1
,解得a=1所以 f(x)=2x+2-|x|
当存在x0∈[1,2]时,使不等式2xf(2x)+mf(x)≥0恒成立,即23x+2-x+m(2x+2-x)≥0成立,
即24x+1+m(22x+1)≥0成立,即-m≤
 =22x+1-2+
=22x+1-2+ ≤
≤
故m≥-

故应选B.
点评:本题考点是指数函数的综合题,考查复杂指数式的恒等变形与复杂指数方程的变形,运算量较大,由于本题最后解决的是存在性的问题,要区分开其与恒成立问题的区别.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目