题目内容
已知椭圆C:
+
=1(a>b>O),椭圆C焦距为:2c,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
(I)求椭圆c的方程;
(II)设点P(-
,0),过点P的直线l与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线l的斜率的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
(I)求椭圆c的方程;
(II)设点P(-
| a2 |
| c |
分析:(I)利用以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形,可求几何量,从而可得椭圆的方程;
(II)设直线l的方程,代入椭圆方程,利用韦达定理,进而利用直线F1B2,F1B1的方程,可得G在正方形Q内(包括边界)的充要条件,由此可得直线l斜率的取值范围.
(II)设直线l的方程,代入椭圆方程,利用韦达定理,进而利用直线F1B2,F1B1的方程,可得G在正方形Q内(包括边界)的充要条件,由此可得直线l斜率的取值范围.
解答:解:(I)由题设知,a2=8,b=c,∴b2=
a2=4
∴椭圆C的方程为
+
=1;
(II)点P的坐标为(-4,0),设直线l的方程为y=k(x+4)
如图,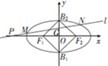
设M(x1,y1),N(x2,y2),线段MN的中点为G(x0,y0),
y=k(x+4)代入椭圆方程,消去y可得(1+2k2)x2+16k2x+32k2-8=0
由△=(16k2)2-4(1+2k2)(32k2-8)>0,可得-
<k<
又x1+x2=-
,
∴x0=
=-
,y0=k(x0+4)=
∵x0=-
≤0,
∴G不可能在y轴的右边
又直线F1B2,F1B1的方程分别为y=x+2,y=-x-2,所以G在正方形Q内(包括边界)的充要条件为
,即
,解得-
≤k≤
,满足-
<k<
故直线l斜率的取值范围是[-
,
].
| 1 |
| 2 |
∴椭圆C的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(II)点P的坐标为(-4,0),设直线l的方程为y=k(x+4)
如图,

设M(x1,y1),N(x2,y2),线段MN的中点为G(x0,y0),
y=k(x+4)代入椭圆方程,消去y可得(1+2k2)x2+16k2x+32k2-8=0
由△=(16k2)2-4(1+2k2)(32k2-8)>0,可得-
| ||
| 2 |
| ||
| 2 |
又x1+x2=-
| 16k2 |
| 1+2k2 |
∴x0=
| x1+x2 |
| 2 |
| 8k2 |
| 1+2k2 |
| 4k |
| 1+2k2 |
∵x0=-
| 8k2 |
| 1+2k2 |
∴G不可能在y轴的右边
又直线F1B2,F1B1的方程分别为y=x+2,y=-x-2,所以G在正方形Q内(包括边界)的充要条件为
|
|
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故直线l斜率的取值范围是[-
| ||
| 2 |
| ||
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目