题目内容
△ABC的外接圆的直径为1,三个内角A、B、C的对边为a、b、c, =(cosA,-b),a≠b,已知
=(cosA,-b),a≠b,已知 ⊥
⊥ 。
。
(1)求sinA+sinB的取值范围;
(2)若abx=a+b,试确定实数x的取值范围.
 =(cosA,-b),a≠b,已知
=(cosA,-b),a≠b,已知 ⊥
⊥ 。
。(1)求sinA+sinB的取值范围;
(2)若abx=a+b,试确定实数x的取值范围.
解:(1)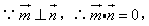 即
即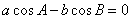 ,
,
由正弦定理,知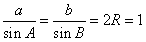 ,
,
∴a=sinA,b=sinB,∴sinAcosA=sinBcosB,∴sin2A=sin2B,
∵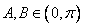 ,
,
∴2A=2B或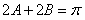 ,
,
∴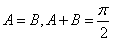 ,
,
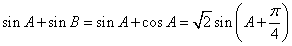 ,
,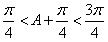 ,
,
∴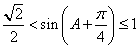 ,
,
∴sinA+sinB的取值范围为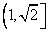 。
。
(2)∵abx=a+b,
∴sinA·sinB·x=sinA+sinB,
∴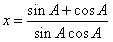 ,
,
令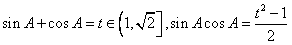 ,
,
∴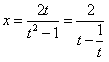 ,
,
∵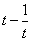 在
在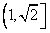 上单调递增,∴
上单调递增,∴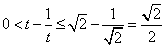 ,
,
∴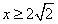 ,故x的取值范围为
,故x的取值范围为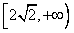 。
。
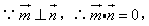 即
即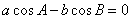 ,
,由正弦定理,知
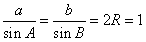 ,
,∴a=sinA,b=sinB,∴sinAcosA=sinBcosB,∴sin2A=sin2B,
∵
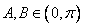 ,
,∴2A=2B或
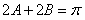 ,
,∴
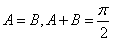 ,
,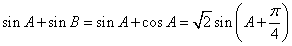 ,
,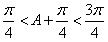 ,
,∴
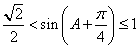 ,
,∴sinA+sinB的取值范围为
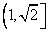 。
。(2)∵abx=a+b,
∴sinA·sinB·x=sinA+sinB,
∴
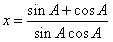 ,
,令
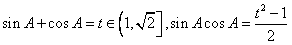 ,
, ∴
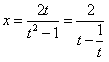 ,
,∵
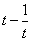 在
在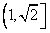 上单调递增,∴
上单调递增,∴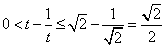 ,
, ∴
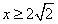 ,故x的取值范围为
,故x的取值范围为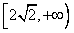 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
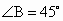 ,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.
,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.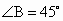 ,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.
,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.