题目内容
已知函数 .
.(1)若a=-4,求函数f(x)的单调区间;
(2)设函数
 ,试问:在定义域内是否存在三个不同的自变量的取值xi(i=1,2,3)使得f(xi)-g(xi)的值恰好都相等,若存在,请求出a的范围,若不存在,请说明理由?
,试问:在定义域内是否存在三个不同的自变量的取值xi(i=1,2,3)使得f(xi)-g(xi)的值恰好都相等,若存在,请求出a的范围,若不存在,请说明理由?
【答案】分析:(1)由a=-4, =
= ,由此能求出函数f(x)的单调区间.
,由此能求出函数f(x)的单调区间.
(2)若定义域内存在三个不同的自变量的取值xi(i=1,2,3),使得f(xi)-g(xi)的值恰好都相等,设f(xi)-g(xi)=m.(i=1,2,3),则对于某一实数m,方程f(x)-g(x)=m在(0,+∞)上有三个不等的实数,由此能求出在定义域内不存在三个不同的自变量的取值xi(i=1,2,3)使得f(xi)-g(xi)的值恰好都相等.
解答:解:(1)∵ .
.
∴ ,
,
∵a=-4,∴ =
= ,
,
由x>0,f′(x)=0,得x=1.
当0<x<1时,f′(x)<0;当x>1时,f′(x)>0.
∴函数f(x)的单调减区间为(0,1),单调增区间为(1,+∞).
(2)若定义域内存在三个不同的自变量的取值xi(i=1,2,3),
使得f(xi)-g(xi)的值恰好都相等,
设f(xi)-g(xi)=m.(i=1,2,3),
则对于某一实数m,方程f(x)-g(x)=m在(0,+∞)上有三个不等的实数,
设F(x)=f(x)-g(x)=x2+ -(
-( ),
),
=x2+ +
+ ,
,
则 ,x>0至少有两个不同的零点,
,x>0至少有两个不同的零点,
即a=-(4x2-2xsin2x),x>0至少有两个不同的解,
设G(x)=4x2-2xsin2x,x>0
则G′(x)=8x-2sin2x-4xcos2x
=2(2x-sin2x)+4x(1-cos2x),
设h(x)=2x-sin2x,
则h′(x)=2-2cos2x≥0,
故h(x)在(0,+∞)上单调递增,
则当x>0时,h(x)>h(0)=0,
即2x>sin2x,
又1-cos2x>0,
则G′(x)>0,故G(x)在(0,+∞)上是增函数,
a=-(4x2-2xsin2x),x>0至多只有一个解,故不存在.
点评:本题考查函数的单调区间的求法,考查满足条件的实数的取值范围的求法.综合性强,难度大,具有一定的探索性.解题时要认真审题,仔细解答,注意合理地进行等价转化.
 =
= ,由此能求出函数f(x)的单调区间.
,由此能求出函数f(x)的单调区间.(2)若定义域内存在三个不同的自变量的取值xi(i=1,2,3),使得f(xi)-g(xi)的值恰好都相等,设f(xi)-g(xi)=m.(i=1,2,3),则对于某一实数m,方程f(x)-g(x)=m在(0,+∞)上有三个不等的实数,由此能求出在定义域内不存在三个不同的自变量的取值xi(i=1,2,3)使得f(xi)-g(xi)的值恰好都相等.
解答:解:(1)∵
 .
.∴
 ,
,∵a=-4,∴
 =
= ,
,由x>0,f′(x)=0,得x=1.
当0<x<1时,f′(x)<0;当x>1时,f′(x)>0.
∴函数f(x)的单调减区间为(0,1),单调增区间为(1,+∞).
(2)若定义域内存在三个不同的自变量的取值xi(i=1,2,3),
使得f(xi)-g(xi)的值恰好都相等,
设f(xi)-g(xi)=m.(i=1,2,3),
则对于某一实数m,方程f(x)-g(x)=m在(0,+∞)上有三个不等的实数,
设F(x)=f(x)-g(x)=x2+
 -(
-( ),
),=x2+
 +
+ ,
,则
 ,x>0至少有两个不同的零点,
,x>0至少有两个不同的零点,即a=-(4x2-2xsin2x),x>0至少有两个不同的解,
设G(x)=4x2-2xsin2x,x>0
则G′(x)=8x-2sin2x-4xcos2x
=2(2x-sin2x)+4x(1-cos2x),
设h(x)=2x-sin2x,
则h′(x)=2-2cos2x≥0,
故h(x)在(0,+∞)上单调递增,
则当x>0时,h(x)>h(0)=0,
即2x>sin2x,
又1-cos2x>0,
则G′(x)>0,故G(x)在(0,+∞)上是增函数,
a=-(4x2-2xsin2x),x>0至多只有一个解,故不存在.
点评:本题考查函数的单调区间的求法,考查满足条件的实数的取值范围的求法.综合性强,难度大,具有一定的探索性.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
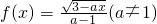 .
.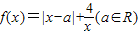 .
.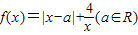 .
.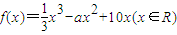 .
.