题目内容
在△ABC总,角A,B,C所对的边分别为a,b,c.已知
=
(1)求角B的大小;
(2)设T=sin2A+sin2C,求T的取值范围.
| sinC |
| sinA |
| a2+c2-b2 |
| a2 |
(1)求角B的大小;
(2)设T=sin2A+sin2C,求T的取值范围.
分析:(1)已知等式左边利用正弦定理化简,整理后利用余弦定理求出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
(2)将T关系式利用二倍角的余弦函数公式化简,整理后用A表示出B,利用两角和与差的余弦函数公式化为一个角的余弦函数,根据A的范围求出这个角的范围,利用余弦函数的图象与性质即可求出T的范围.
(2)将T关系式利用二倍角的余弦函数公式化简,整理后用A表示出B,利用两角和与差的余弦函数公式化为一个角的余弦函数,根据A的范围求出这个角的范围,利用余弦函数的图象与性质即可求出T的范围.
解答:解:(1)已知等式利用正弦定理化简得:
=
,
整理得:
=
,即cosB=
,
∵B为三角形的内角,∴B=60°;
(2)T=sin2A+sin2C=
(1-cos2A)+
(1-cos2C)
=1-
(cos2A+cos2C)=1-
[cos2A+cos(240°-2A)]=1-
(
cos2A-
sin2A)
=1-
cos(2A+60°),
∵0<A<120°,∴60°<2A+60°<300°,
∴-1≤cos(2A+60°)<
,
则
<T≤
.
| c |
| a |
| a2+c2-b2 |
| a2 |
整理得:
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
| 1 |
| 2 |
∵B为三角形的内角,∴B=60°;
(2)T=sin2A+sin2C=
| 1 |
| 2 |
| 1 |
| 2 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=1-
| 1 |
| 2 |
∵0<A<120°,∴60°<2A+60°<300°,
∴-1≤cos(2A+60°)<
| 1 |
| 2 |
则
| 3 |
| 4 |
| 3 |
| 2 |
点评:此题考查了正弦、余弦定理,二倍角的余弦函数公式,两角和与差的余弦函数公式,以及余弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
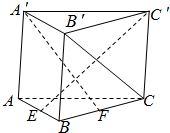 如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图直三棱柱ABC-A′B′C′的侧棱长为3,AB⊥BC,且AB=BC=3,点E,F分别是棱AB,BC上的动点,且AE=BF. 如图所示,已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,AB=
如图所示,已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,AB=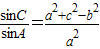
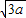 ,E,F分别是AC,AD上的动点,且
,E,F分别是AC,AD上的动点,且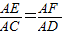 =λ(0<λ<1).
=λ(0<λ<1).