题目内容
正方形ABCD中，E、F为AB、CD的中点，M、N为AD、BC的中点，将正方形沿MN折成一个直二面角，则异面直线MF与NE所成角的大小为（ ）
分析：由已知可以E为坐标原点，EB，EF，EA分别为x，y，z轴正方向建立空间坐标系，设正方形ABCD中边长为2，分别求出各点的坐标，进而求出向量
，
的坐标，代入向量夹角公式，可得答案．
| MF |
| NE |
解答：
解：如图所示，
以E为坐标原点，EB，EF，EA分别为x，y，z轴正方向建立空间坐标系
设正方形ABCD中边长为2
则E（0，0，0），F（0，2，0），N（1，1，0），M（0，1，1）
∴
=（0，1，-1），
=（-1，-1，0）
令异面直线MF与NE所成角为θ
则cosθ=
=
=
故θ=
故选A
解：如图所示，以E为坐标原点，EB，EF，EA分别为x，y，z轴正方向建立空间坐标系
设正方形ABCD中边长为2
则E（0，0，0），F（0，2，0），N（1，1，0），M（0，1，1）
∴
| MF |
| NE |
令异面直线MF与NE所成角为θ
则cosθ=
|
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
故θ=
| π |
| 3 |
故选A
点评：本题考查的知识点是异面直线的夹角，建立空间坐标系，将异面直线的夹角转化为向量的夹角是解答的关键．
练习册系列答案
相关题目
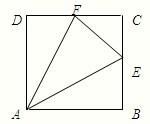如图，正方形ABCD中，E，F分别为BC，CD的中点，设∠EAF=θ，则cosθ=
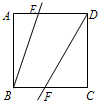（2012•浙江模拟）如图，在正方形ABCD中，E，F分别为线段AD，BC上的点，∠ABE=20°，∠CDF=30°．将△ABE绕直线BE、△CDF绕直线CD各自独立旋转一周，则在所有旋转过程中，直线AB与直线DF所成角的最大值为