题目内容
已知函数
．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）在△ABC中，三内角A，B，C的对边分别为a，b，c，已知
成等差数列，且
=9，求a的值．
解：（I）f（x）=
=
sin2x+
cos2x=sin（2x+
）．
令 2kπ﹣
≤（2x+
）≤2kπ+
，可得 kπ﹣
≤x≤kπ+，k∈z．
即f（x）的单调递增区间为[kπ﹣，kπ+]，k∈z．
（II）在△ABC中，由
，可得sin（2A+）=
，∵
＜2A+＜2π+，
∴2A+= 或
，∴A=
（或A=0 舍去）．
∵b，a，c成等差数列可得 2a=b+c，∵
=9，∴bccosA=9，即bc=18．
由余弦定理可得 a2=b2+c2﹣2bc•cosA=（b+c）2﹣3bc=4a2﹣54，
求得a2=18，∴a=3
．
练习册系列答案
相关题目
某同学用“五点法”画函数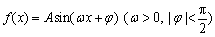
在某一个周期内的图象时，列表并填入了部分数据，如下表：
|
| 0 |
|
|
|
|
|
|
|
| |||
|
| 0 | 5 |
| 0 |
（Ⅰ）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数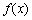
的解析式；
（Ⅱ）令g(x)=f (x+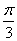
）—1，当x∈[—
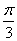，] 时，若存在g(x)＜a—2成立，求实数a的取值范围.
中，
，
，
的对边分别为
，
，
，若
，
，
，则
___ ______．
，则a+b的值是（）
的值为（ ）
，曲线
经过点
，现将一质点随机投入长方形
中，则质点落在图中阴影区域的概率是（ ）
B．
C．
D．
B.
C.
D.
