题目内容
(本题满分12分)设平面直角坐标系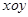 中,设二次函数
中,设二次函数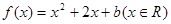 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(1)求实数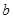 的取值范围;
的取值范围;
(2)求圆C 的方程;
(3)问圆C 是否经过某定点(其坐标与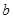 无关)?请证明你的结论.
无关)?请证明你的结论.
(1)
(2)
(3)圆恒过点(0,1)
解析试题分析:解:(1)由题意可知,方程 有两不等3根,
有两不等3根,
(2)设圆C 的方程为:
圆C与 轴的交点和二次函数
轴的交点和二次函数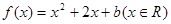 的图象与
的图象与 轴的交点相同,
轴的交点相同,
所以在圆的方程 中令
中令 ,得
,得 应为
应为 ,所以
,所以 ;
;
因为圆C过点 ,在圆的方程
,在圆的方程 中令
中令 ,得
,得
方程 有根
有根 ,代入得:
,代入得: ,
,
所求圆C的方程为:
(3)圆C的方程可改写为: ,所以圆恒过点(0,1)。
,所以圆恒过点(0,1)。
考点:二次函数,圆的方程
点评:解决该试题的关键是利用一般是待定系数法求解圆的方程,属于基础题。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;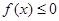 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求