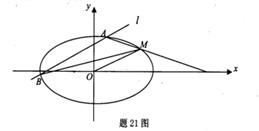
题目内容
已知离心率为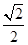 的椭圆
的椭圆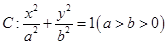 过点
过点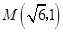 ,
,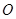 是坐
是坐
标原点.
(1)求椭圆 的方程;
的方程;
(2)已知点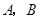 为椭圆
为椭圆 上相异两点,且
上相异两点,且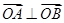 ,判定直线
,判定直线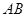 与圆
与圆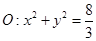 的
的
位置关系,并证明你的结论.
【答案】
(1) 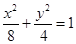
(2) 相切,证明略
【解析】(1)由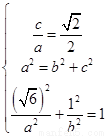 ,解得:
,解得: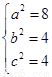 故椭圆
故椭圆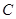 的方程为
的方程为
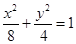
(2)设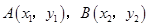 ,直线
,直线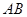 的方程为:
的方程为: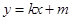
由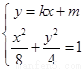 ,得:
,得: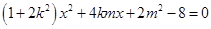
则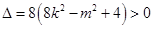 ,即
,即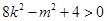 由韦达定理得:
由韦达定理得:

则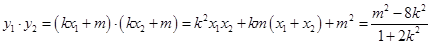 由
由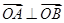 得:
得:
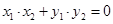 ,
,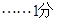
即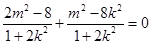 ,化简得:
,化简得: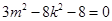
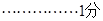
因为圆心到直线的距离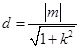 ,
,
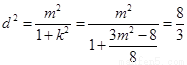 而
而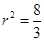 ,
,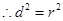 ,即
,即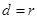
此时直线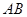 与圆
与圆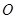 相切。
相切。
当直线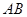 的斜率不存在时,由
的斜率不存在时,由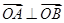 可以计算得
可以计算得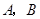 的坐标为
的坐标为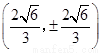 或
或
 此时直线
此时直线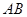 的方程为
的方程为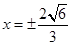
满足圆心到直线的距离等于半径,即直线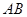 与圆
与圆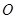 相切
相切
综上,直线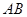 与圆
与圆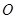 相切
相切

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
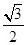 的椭圆
的椭圆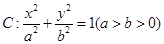 过点
过点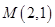 ,
,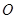 为坐标原点,平行于
为坐标原点,平行于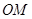 的直线
的直线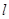 交椭圆于
交椭圆于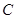 不同的两点
不同的两点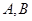 。
。
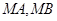 的斜率分别为
的斜率分别为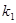 、
、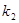 ,求证:
,求证: 的椭圆
的椭圆 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
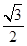 的椭圆
的椭圆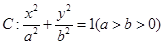 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线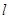 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。 面积的最大值;
面积的最大值;