题目内容
(1)选修4-4:坐标系与参数方程
在曲线C1:
(θ为参数)上求一点,使它到直线C2:
(t参数)
的距离最小,并求出该点坐标和最小距离.
(2)选修4-5;不等式选讲
若ab>0,且A(a,0),B(0,b),C(-2,-2)三点共线,求ab的最小值.
在曲线C1:
|
|
的距离最小,并求出该点坐标和最小距离.
(2)选修4-5;不等式选讲
若ab>0,且A(a,0),B(0,b),C(-2,-2)三点共线,求ab的最小值.
(1)直线C2化成普通方程是x+y+2
-1=0.
设所求的点为P(1+cosθ,sinθ),则P到直线C2的距离d=
=|sin(θ+
)+2|
当θ+
=
+2kπ,k∈Z时,即θ=
+2kπ,k∈Z时,d取最小值1,
此时,点P的坐标是(1-
,-
).
(2)根据题意,
=
,即ab=-2(a+b),
∵ab>0,∴a<0,b<0,∴(-a)+(-b)≥2
∴ab≥4
,∴
≥4或
≤0,∴ab≤16,当且仅当a=b-4时等号成立,∴(ab)min=16
| 2 |
设所求的点为P(1+cosθ,sinθ),则P到直线C2的距离d=
|1+cosθ+sinθ+2
| ||
|
| π |
| 4 |
当θ+
| π |
| 4 |
| 3π |
| 2 |
| 5π |
| 4 |
此时,点P的坐标是(1-
| ||
| 2 |
| ||
| 2 |
(2)根据题意,
| 2 |
| a+2 |
| b+2 |
| 2 |
∵ab>0,∴a<0,b<0,∴(-a)+(-b)≥2
| (-a)(-b), |
∴ab≥4
| ab |
| ab |
| ab |

练习册系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲 .
. (α为参数),点Q极坐标为
(α为参数),点Q极坐标为 .
. .
. (α为参数),点Q极坐标为
(α为参数),点Q极坐标为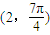 .
.