题目内容
确定函数f(x)=log x+x-4的零点个数.
x+x-4的零点个数.
解:设y1=log x,y2=4-x,则f(x)的零点个数即y1与y2的交点个数,
x,y2=4-x,则f(x)的零点个数即y1与y2的交点个数,
作出两函数图象,如图.
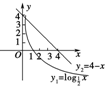
由图知,y1与y2在区间(0,1)内有一个交点,
当x=4时,y1=-2,y2=0,
当x=8时,y1=-3,y2=-4,
∴在(4,8)内两曲线又有一个交点,
∴两曲线只有两个交点,
即函数f(x)=log x+x-4有两个零点.
x+x-4有两个零点.
分析:由题意,判断此函数的零点个数可转化为两个函数y1=log x,y2=4-x,的交点个数结合两个函数的图象得出两函数图象的交点个数,即可得到原函数零点的个数.
x,y2=4-x,的交点个数结合两个函数的图象得出两函数图象的交点个数,即可得到原函数零点的个数.
点评:本题考查函数的零点的定义及其个数的判断,解题的关键是理解函数的零点定义,依据定义将求零点个数的问题转化为两个函数交点个数的问题.
 x,y2=4-x,则f(x)的零点个数即y1与y2的交点个数,
x,y2=4-x,则f(x)的零点个数即y1与y2的交点个数,作出两函数图象,如图.

由图知,y1与y2在区间(0,1)内有一个交点,
当x=4时,y1=-2,y2=0,
当x=8时,y1=-3,y2=-4,
∴在(4,8)内两曲线又有一个交点,
∴两曲线只有两个交点,
即函数f(x)=log
 x+x-4有两个零点.
x+x-4有两个零点.分析:由题意,判断此函数的零点个数可转化为两个函数y1=log
 x,y2=4-x,的交点个数结合两个函数的图象得出两函数图象的交点个数,即可得到原函数零点的个数.
x,y2=4-x,的交点个数结合两个函数的图象得出两函数图象的交点个数,即可得到原函数零点的个数.点评:本题考查函数的零点的定义及其个数的判断,解题的关键是理解函数的零点定义,依据定义将求零点个数的问题转化为两个函数交点个数的问题.

练习册系列答案
相关题目
若函数f(x)=
eax的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
| 1 |
| b |
| A、在圆内 |
| B、在圆上 |
| C、在圆外 |
| D、不确定,与a,b的取值有关 |