Question

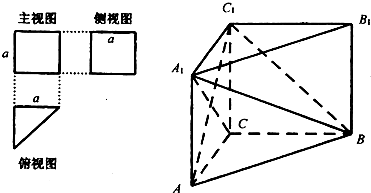
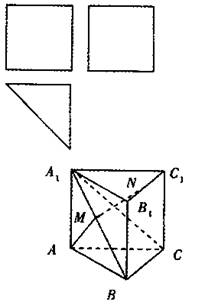
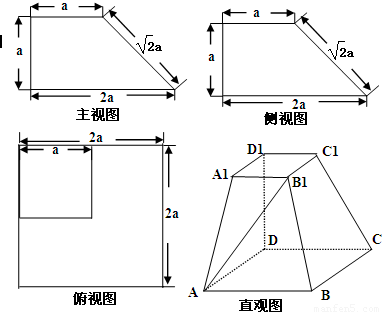
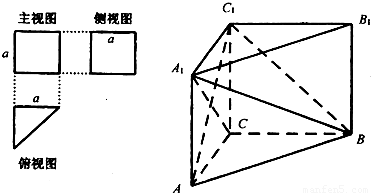
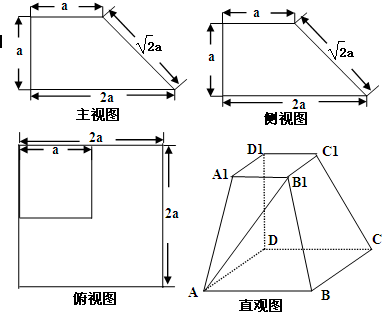
一个多面体的三视图及直观图如图所示：
（Ⅰ）求异面直线AB₁与DD₁所成角的余弦值：
（Ⅱ）试在平面ADD₁A₁中确定一个点F，使得FB₁⊥平面BCC₁B₁；
（Ⅲ）在（Ⅱ）的条件下，求二面角F-CC₁-B的余弦值．

Answer 1

解；依题意知，该多面体为底面是正方形的四棱台，且D₁D⊥底面ABCD，AB=2A₁B₁=2DD₁=2a…（2分）
以D为原点，DA、DC、DD₁所在的直线为x，y，z轴，
建立如图所示的空间直角坐标系，则D（0，0，0），A（2a，0，0），B₁（a，a，a），D₁（0，0，a），B（2a，2a，0），C（0，2a，0），C₁（0，a，a）…（4分）
（Ⅰ）∵

AB1

=（-a，a，a），

DD1

=（0，0，a）
∴cos＜

AB1

，

DD1

＞=

AB1 • DD1

| AB1 || DD1 |

=

3

3

即直线AB₁与DD₁所成角的余弦值为

3

3

…（6分）
（II）设F（x，0，z），∵

BB1

=（-a，a，a），

BC

=（-2a，0，0），

FB1

=（a-x，a，a-z）
由FB₁⊥平面BCC₁B₁得
即

-a(a-x)-a2+a(a-z)=0 -2a(a-x)

得

x=a z=0

∴F（a，0，0）即F为DA的中点…（9分）
（III）由（II）知

FB1

为平面BCC₁B₁的法向量．
设

n

=（x₁，y₁，z，）为平面FCC₁的法向量．
∵

CC1

=（0，-a，a），

FC

=）-a，2a，0）
∴

-ay1+az1=0 -ax1+2ay1=0

令y₁=1得x₁=2，z₁=1
∴

n

=（2，1，1）
∴cos＜

n

，

FB1

＞=

n • FB1

n || FB1 |

=

3

3

即二面角F-CC₁-B的余弦值为

3

3

…（12分）