题目内容
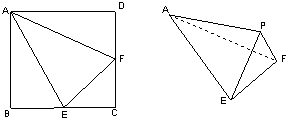 (2008•海珠区一模)正方形ABCD的边长为1,分别取边BC,CD的中点E,F,连接AE,EF,AF,以AE,EF,AF为折痕,折叠这个正方形,使点B,C,D重合于一点P,得到一个四面体,如图所示.
(2008•海珠区一模)正方形ABCD的边长为1,分别取边BC,CD的中点E,F,连接AE,EF,AF,以AE,EF,AF为折痕,折叠这个正方形,使点B,C,D重合于一点P,得到一个四面体,如图所示.(1)求证:AP⊥EF;
(2)求证:平面APE⊥平面APF;
(3)求三棱锥P-AEF的体积.
分析:(1)通过∠APE=∠APF=90°,证明PA⊥平面PEF,然后证明AP⊥EF;
(2)利用∠APE=∠EPF=90°,证明PE⊥平面APF,然后证明平面APE⊥平面APF;
(3)利用VP-AEF=VA-PEF=
S△PEF•AP,求出几何体的体积.
(2)利用∠APE=∠EPF=90°,证明PE⊥平面APF,然后证明平面APE⊥平面APF;
(3)利用VP-AEF=VA-PEF=
| 1 |
| 3 |
解答:(本小题满分14分)
证明:(1)∵∠APE=∠APF=90°,
PE∩PF=P,
∴PA⊥平面PEF.…(3分)
又EF?平面PEF,
AP⊥EF;…5分
(2)∵∠APE=∠EPF=90°,AP∩PF=P,
∴PE⊥平面APF.…(8分)
又PE?平面APE,
∴平面APE⊥平面APF.…(10分)
(3)由(1)知PA⊥平面PEF,
∴VP-AEF=VA-PEF=
S△PEF•AP=
×
×
×
×1=
.…(14分)
证明:(1)∵∠APE=∠APF=90°,
PE∩PF=P,
∴PA⊥平面PEF.…(3分)
又EF?平面PEF,
AP⊥EF;…5分
(2)∵∠APE=∠EPF=90°,AP∩PF=P,
∴PE⊥平面APF.…(8分)
又PE?平面APE,
∴平面APE⊥平面APF.…(10分)
(3)由(1)知PA⊥平面PEF,
∴VP-AEF=VA-PEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 24 |
点评:本小题主要考查空间线面关系,体积的求法,考查空间想像能力和推理论证能力,考查计算能力.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
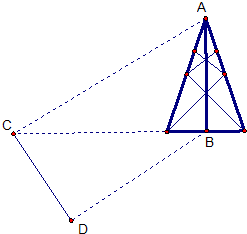 (2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB.
(2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB. (2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )
(2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )