题目内容
已知a>0,设命题p:函数y=ax在R上单调递减,q:设函数y=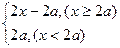 ,函数y>1恒成立, 若p∧q为假,p∨q为真,求a的取值范围
,函数y>1恒成立, 若p∧q为假,p∨q为真,求a的取值范围
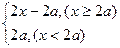 ,函数y>1恒成立, 若p∧q为假,p∨q为真,求a的取值范围
,函数y>1恒成立, 若p∧q为假,p∨q为真,求a的取值范围0<a≤ 或a≥1
或a≥1
 或a≥1
或a≥1若p是真命题,则0<a<1,
若q是真命题,则函数y>1恒成立,即函数y的最小值大于1,而函数y的最小值为2a,
只需2a>1,∴a> ,∴q为真命题时a>
,∴q为真命题时a> ,
,
又∵p∨q为真,p∧q为假,∴p与q一真一假.
若p真q假,则0<a≤ ;若p假q真,则a≥1.
;若p假q真,则a≥1.
故a的取值范围为0<a≤ 或a≥1
或a≥1
若q是真命题,则函数y>1恒成立,即函数y的最小值大于1,而函数y的最小值为2a,
只需2a>1,∴a>
 ,∴q为真命题时a>
,∴q为真命题时a> ,
, 又∵p∨q为真,p∧q为假,∴p与q一真一假.
若p真q假,则0<a≤
 ;若p假q真,则a≥1.
;若p假q真,则a≥1. 故a的取值范围为0<a≤
 或a≥1
或a≥1 
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 :
: ,
, ,则 ( )
,则 ( ) :
:

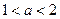 ,设命题
,设命题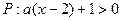 ,命题
,命题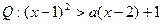 ,非P∨非Q是假命题,求
,非P∨非Q是假命题,求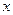 的集合。
的集合。 ,则
,则 全为0 .
全为0 . 是偶数,则
是偶数,则 都是偶数.
都是偶数. ,则
,则
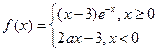 (
(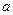 为常数,且
为常数,且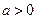 ),对于下列命题:
),对于下列命题: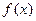 在每一点处都连续;
在每一点处都连续;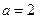 ,则函数
,则函数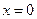 处可导;
处可导;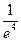 ;
;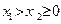 ,恒有
,恒有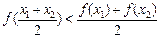 .
.