题目内容
【题目】已知函数y=f（x）（x＞0）满足：f（xy）=f（x）+f（y），当x＜1时f（x）＞0，且f（ 
）=1；
（1）证明：y=f（x）是（x＞0）上的减函数；
（2）解不等式f（x﹣3）＞f（ 
）﹣2．
【答案】
（1）证明：设0＜x1＜x2，则0＜ 
＜1，
由题意f（x1）﹣f（x2）=f（ x2）﹣f（x2）=f（ ）+f（x2）﹣f（x2）=f（ ）＞0，
则f（x1）＞f（x2），
∴y=f（x）是（x＞0）上的减函数
（2）解：由函数的定义域知：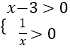 
，解得x＞3；
又∵f（ 
）=1，
∴f（ 
）=f（ × ）=f（ ）+f（ ）=1+1=2，
由f（x﹣3）＞f（ 
）﹣2．得f（x﹣3）+2＞f（ ），
∴f（x﹣3）+f（ ）＞f（ ），f（ 
）＞f（ ），
由（2）得 ＜ ，解得﹣1＜x＜4，
综上知3＜x＜4为所求
【解析】1、本题考查的是函数单调性的定义。设0＜x1＜x2，则0＜ x1 x2 ＜1，由题意f（x1）﹣f（x2）=f（ x2）﹣f（x2）=f（ ）+f（x2）﹣f（x2）=f（ ）＞0，则f（x1）＞f（x2），即y=f（x）是（x＞0）上的减函数
2、由题意可得∵f （）=1，∴f（ 
）=f（ × ）=f（ ）+f（ ）=1+1=2，由f（x﹣3）＞f（ ）﹣2．得f（x﹣3）+2＞f（ ），
∴f（x﹣3）+f（ ）＞f（ ），f（ ）＞f（ ），由（2）得 ＜ ，解得﹣1＜x< 4.
练习册系列答案
相关题目
