题目内容
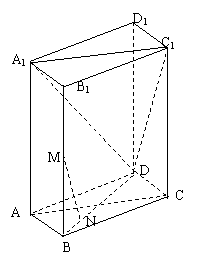
(本小题14分)如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=90°.M是BB1的中点,N在BD上,3BN=ND
 (Ⅰ)证明:
(Ⅰ)证明:![]() ∥平面A1DC1;
∥平面A1DC1;
(Ⅱ)求二面角D—A1A—C的大小;
解:(1)取AB的中点H,BC的中点G,连接MH、HG、MG,∵3BN=ND ∴N是OB的中点
∴MG过N点∵HG∥AC,AC∥A1C1∴HG∥A1C1 又∵HG不在平面DA1C1,
![]() 平面DA1C1 ∴HG∥平面DA1C1同理可证得MG∥平面DA1C1 又∵MG∩HG=G
平面DA1C1 ∴HG∥平面DA1C1同理可证得MG∥平面DA1C1 又∵MG∩HG=G
∴平面MGH∥平面DA1C1∵MN![]() 平面MGH ∴MN∥平面DA1C…………………… 7分
平面MGH ∴MN∥平面DA1C…………………… 7分
(2) ∵平面AA1C1C⊥平面ABCD 且两平面的交线为AC,又∠A1AC=90°
∴A1A⊥平面ABCD∴A1A⊥AC, A1A⊥AD ∴∠DAC是二面角D—A1A—C的平面角∵四边形ABCD是菱形 且∠ABC=60°,∴∠BAC=1200,又因为菱形对角线平分内角,∴∠DAC=600 ∴二面角D—A1A—C的大小为600
【命题意图】考查空间向量运用,垂直关系证明,求二面角

练习册系列答案
相关题目
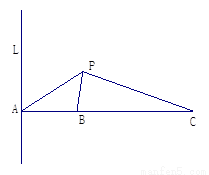
 km,用
km,用 的面积为14,
的面积为14, 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且


 ,
, 与
与 交于
交于 。设存在
。设存在 和
和 使
使 ,
, ,
, ,
, 。
。  ,
, 表示
表示
 的面积
的面积 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱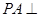 底面
底面 为
为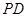 的中点.
的中点.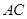 与
与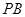 所成角的余弦值;
所成角的余弦值;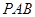 内找一点
内找一点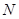 ,使
,使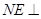 平面
平面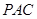 ,并分别求出点
,并分别求出点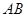 和
和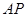 的距离.
的距离.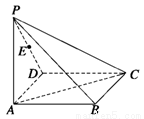
 中,
中, 平面
平面 ,
, ,
, ,
, 分别是
分别是 上
上 平面
平面 为
为 .
. 平面
平面 ;
; ,求直线
,求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值. 中,
中, ,点
,点 在边
在边 上,
上, 。
。 平面
平面 ;
; 是
是 的中点,求证:
的中点,求证: 平面
平面 .
.