题目内容
设非空集合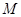 同时满足下列两个条件:
同时满足下列两个条件:
① ;
;
②若 ,则
,则 ,
, .则下列结论正确的是
.则下列结论正确的是
A.若 为偶数,则集合 为偶数,则集合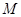 的个数为 的个数为 个; 个; |
B.若 为偶数,则集合 为偶数,则集合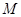 的个数为 的个数为 个; 个; |
C.若 为奇数,则集合 为奇数,则集合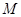 的个数为 的个数为 个; 个; |
D.若 为奇数,则集合 为奇数,则集合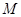 的个数为 的个数为 个. 个. |
B
解析试题分析:当 时,
时, ,且满足
,且满足 ,故集合
,故集合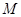 的个数为1个;当
的个数为1个;当 时,
时, ,且
,且 ,故集合
,故集合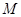 的个数为1个;当
的个数为1个;当 时,
时, ,且
,且 ,
, ,故集合
,故集合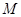 的个数为3个,故可排除A,C,D,选B.
的个数为3个,故可排除A,C,D,选B.
考点:1、子集;2、归纳推理.

练习册系列答案
相关题目
若集合 ,则
,则 ( )
( )
A. | B. |
C. | D. |
定义集合 与
与 的运算“*”为:
的运算“*”为: 或
或 ,但
,但 ,按此定义,
,按此定义, ( )
( )
A. | B. | C. | D. |
已知 ,
, ,则
,则 的元素个数为( )
的元素个数为( )
| A.1 | B.2 | C.3 | D.4 |
已知集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知集合 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
设函数 的定义域为
的定义域为 ,函数
,函数 的定义域为
的定义域为 ,则( )
,则( )
A. | B. | C. | D. |
设集合 ,
, ,,则
,,则 ( )
( )
A. | B. | C. | D. |