Question

设椭圆=1(a＞b＞0)的焦点分别为F₁(-1,0)、F₂(1,0),右准线l交x轴于点A,且.

(1)试求椭圆的方程;

(2)过F₁、F₂分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形DMEN面积的最大值和最小值.

(文)已知函数f(x)=x³+bx²+cx,b、c∈R,且函数f(x)在区间(-1,1)上单调递增,在区间(1,3)上单调递减.

(1)若b=-2,求c的值;

(2)求证:c≥3;

(3)设函数g(x)=f′(x),当x∈［-1,3］时,g(x)的最小值是-1,求b、c的值.

Answer 1

解:(1)由题意,||=2c=2,

∴A(a²,0).                                                              

∵,

∴F₂为AF₁的中点.                                                      

∴a²=3,b²=2,

即椭圆方程为=1.                                                 

(2)当直线DE与x轴垂直时,|DE|=2,

此时|MN|=2a=,四边形DMEN的面积为=4.

同理当MN与x轴垂直时,也有四边形DMEN的面积为=4.         

当直线DE、MN均与x轴不垂直时,

设DE:y=k(x+1),

代入椭圆方程,消去y得

(2+3k²)x²+6k²x+(3k²-6)=0.

设D(x₁,y₁),E(x₂,y₂),

则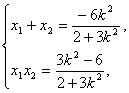                                                   

∴|x₁-x₂|=.

∴|DE|=|x₁-x₂|=.

同理,|MN|=.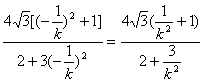                               

∴四边形的面积

S=.        

令u=k²+,得S=,

∵u=k²+≥2,

当k=±1时,u=2,S=,且S是以u为自变量的增函数,

∴≤S＜4.

综上,可知四边形DMEN面积的最大值为4,最小值为.                     

(文)解:(1)由已知可得f′(1)=0,                                            

又f′(x)=x²+2bx+c,

∴f′(1)=1+2b+c=0.                                                       

将b=-2代入,可得c=3.                                                    

(2)证明:由(1)可知b=,代入f′(x)可得f′(x)=x²-(c+1)x+c.

令f′(x)=0,则x₁=1,x₂=c,                                                   

又当-1＜x＜1时,f′(x)≥0;

当1＜x＜3时,?f′(x)≤0.

如图所示.

易知c≥3.                                                               

(3)若1≤-b≤3,则

g(x)_min=g(-b)=b²-2b²+c=-1.

又1+2b+c=0,得b=-2或b=0(舍),c=3.

若-b≥3,则g(x)_min=g(3)=9+6b+c=-1,

又1+2b+c=0,得b=(舍).

综上所述,b=-2,c=3.