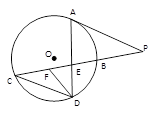
题目内容
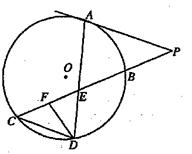
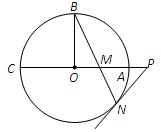
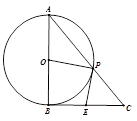
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且DE2 = EF·EC.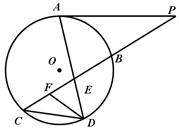
(Ⅰ)求证:CE·EB = EF·EP;
(Ⅱ)若CE:BE = 3:2,DE = 3,EF = 2,求PA的长.

(I)证得 ∽
∽
∴
根据 ,得到
,得到 。
。
(II) 。
。
解析试题分析:
(I)∵ ,
,
∴ ,
,
又∵ ,∴
,∴ ,
,
∴ ∽
∽
∴
又∵ ,
,
∴ 5分
5分
(II) ,
, ,
,
 是⊙
是⊙ 的切线,
的切线, ,
, 10分
10分
考点:相交弦定理、切割定理、三角形相似。
点评:中档题,作为选考内容,难度不大,主要涉及圆与三角形相似的基础知识。

练习册系列答案
相关题目
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于E点,F为CE上一点,且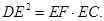
(1)求证:A、P、D、F四点共圆;
(2)若AE·ED=24,DE=EB=4,求PA的长。
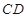 为△
为△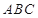 外接圆的切线,
外接圆的切线,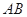 的延长线交直线
的延长线交直线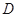 ,
,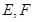 分别为弦
分别为弦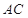 上的点,且
上的点,且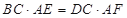 ,
,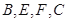 四点共圆.
四点共圆. 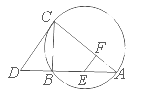
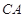 是△
是△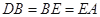 ,求过
,求过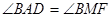 :
: .
.






 ,OA=
,OA=
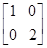 ,N=
,N=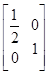 ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.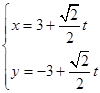 (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.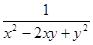 ≥2y+3.
≥2y+3. 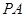 与⊙
与⊙ 相切,
相切, 为切点,
为切点,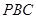 为割线,弦
为割线,弦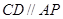 ,
,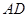 、
、 相交于
相交于 点,
点,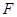 为
为 上一点,且
上一点,且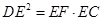
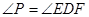 ;
;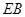 =
=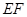 ·
· .
.